Implicitly inverting a function from numerical solution

Question

I have the following piecewise continuous function:

myfun[a_, l1_, l2_] = 
 Piecewise[{{a^2, a < l1}, 
            {a - l1 + l1^2, a >= l1 && a < l2}, 
            {l2 - l1 + l1^2 + Log[a - l2 + 1], a >= l2}}]

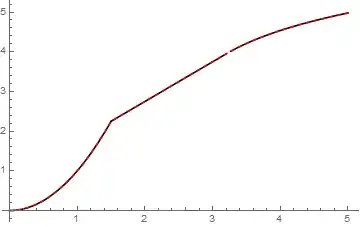
The function is defined by a value $a$ and two parameters $l_1$ and $l_2$ and if I plot it, appears as:

Plot[Evaluate[myfun[a, l1, l2] /. {l1 -> 1.5, l2 -> 3.2}], {a, 0, 5}, PlotRange -> All]

Now, I would like to invert the numerical solution given by $myfun==2.0$ with respect to a, which is a function depending on $l_1$ and $l_2$. I tried to do it "in a delayed way" with

myInvFun[l1_, l2_] := x /. FindRoot[myfun[x, l1, l2] == 2.0, {l, 0}]

But this does not help me, since if I try to plot the following

Plot[Evaluate[myInvFun[l1, l2] /. {l2 -> 3.5}], {l1, 0, 3.5}]

errors appear:

How can I make the inverse function usable as an explicit function even if I use only a definition from numerical solution?

P.S. I had a look to answers like this one and this one but either way I could not find a way to solve my problem

Answer 1

This is simple enough to do analytically.. assuming l2>l1 you can readily find the transition points and invert each piece of the Piecewise expression:

myfuninv[x_, l1_, l2_ /; l2 > l1] = Piecewise[{
   {Sqrt[x], x <= l1^2},
   {x + l1 - l1^2, l1^2 < x <= l2 + l1^2 - l1},
   {Exp[x + l1 - l2 - l1^2] - 1 + l2,  l2 + l1^2 - l1 < x}}]
Plot[ myfuninv[2, l1, 3.5] , {l1, 0, 3.5}]

Answer 2

You can see what you get with the body of your function myInvFun over parameter instances:

In[215]:= FindRoot[myfun[x, 2, 5] == 2.0, {x, 0}]

Out[215]= {x -> 0.}

FindRoot::jsing: Encountered a singular Jacobian at the point {x} = {0.}. 
Try perturbing the initial point(s). >>

So, if you change your definition as advised by the message you'll get results you might expect:

myInvFun[l1_, l2_] := x /. FindRoot[myfun[x, l1, l2] == 2.0, {x, 0.1}]

Plot[Evaluate[myInvFun[l1, 3.5]], {l1, 0, 3.5}]

Answer 3

General Inversion

You can use FindRoot to do a general inversion of a Piecewise function.

The strategy will be to extract the smooth continuous function from the piecewise function and use that as input to FindRoot.

Below is a copy of your function:

myfun[a_, l1_, l2_] = Piecewise[{
   {a^2, a < l1},
   {a - l1 + l1^2, 
    a >= l1 && a < l2}, {l2 - l1 + l1^2 + Log[a - l2 + 1], a >= l2}
   }]

which has three regions that contain three different functions.

Part can be used to access the function that is valid in each region

myfun[a, l1, l2][[1, 1, 1]]
(* a^2 *)

myfun[a, l1, l2][[1, 2, 1]]
(* a - l1 + l1^2 *)

myfun[a, l1, l2][[1, 3, 1]]
(* -l1 + l1^2 + l2 + Log[1 + a - l2] *)

Now we will define the inverse function which takes the limits as well as myfun as input arguments. myfun will be used to set the limits of the inverse Piecewise function as well as being an input to FindRoot.

myInvFun[y_, l1_, l2_, myfun_] := Piecewise[{
   {
    Module[{a, fun},
     fun[a_] = myfun[a, l1, l2][[1, 1, 1]];
     FindRoot[fun[a] == y, {a, l1/2}][[1, 2]]
     ],
    y < myfun[l1, l1, l2]
    },
   {
    Module[{a, fun},
     fun[a_] = myfun[a, l1, l2][[1, 2, 1]];
     FindRoot[fun[a] == y, {a, (l1 + l2)/2}][[1, 2]]
     ],
    y >= myfun[l1, l1, l2] && y < myfun[l2, l1, l2]
    },
   {
    Module[{a, fun},
     fun[a_] = myfun[a, l1, l2][[1, 3, 1]];
     FindRoot[
       l2 - l1 + l1^2 + Log[a - l2 + 1] == y, {a, l2 + 0.5}][[1, 2]]
     ],
    y >= myfun[l2, l1, l2]
    }
   }]

Now myInvFun can be treated like any ordinary function. For example:

myInvFun[2, 1.5, 3.2, myfun]
(* 1.41421 *)

We can validate that the inverse matches myfun by plotting myfun and using ParametricPlot for myInvFun.

Show[
 Plot[myfun[a, 1.5, 3.2], {a, 0, 5}, PlotRange -> All, 
  PlotStyle -> Black],
 ParametricPlot[{myInvFun[y, 1.5, 3.2, myfun], y}, {y, 0, 5}, 
  PlotStyle -> {Red, Dashed}]
 ]

They do indeed match.

Specific Inversion

Clearly you can simply replace the argument a in myFunInv with 2 if you want to plot the inverse as function of l1.

Plot[myInvFun[2, l1, 3.5, myfun], {l1, 0, 3.5}]

Answer 4

The following uses NDSolve to construct interpolations along lines in the domain. We then construct an interpolation between the solutions to NDSolve, which represents a as a function of l1 and l2.

{dadl1, dadl2} = 
  grad = PiecewiseExpand /@ (-D[myfun[a, l1, l2], {{l1, l2}}]/
        D[myfun[a, l1, l2], a]) /. ComplexInfinity -> 0 // Quiet;

sols = Table[
   Block[{l1a = 0, l1b = 3.5, l2},
    Module[{flag = True, res, dl = 0, n = 0},
     While[flag,
      Check[
       l2 = l2b + (-1)^n dl;
       res = 
        NDSolveValue[{a'[l1] == (dadl1 /. a -> a[l1]), a[0] == 2}, 
         a, {l1, l1a, l1b}, PrecisionGoal -> 10]; flag = False,
       flag = True;
       n += 1;
       dl += 0.001]
      ];
     {l2, res}]
    ],
   {l2b, 0., 3.5, 0.1}];

ClearAll[if];
if[sols : {{_?NumericQ, _InterpolatingFunction} ..}] := 
  if[sols[[All, 1]], sols[[All, 2]], 
   Nearest[sols[[All, 1]] -> Automatic]];
if[l2data_, ifns : {__InterpolatingFunction}, nf_NearestFunction][
  l1in_?NumericQ, l2in_?NumericQ] := Module[{i2, $l2, $a},
  {i2[1], i2[2]} = nf[l2in] /. {{1} -> {1, 2},
      {Length@l2data} -> {Length@l2data - 1, Length@l2data},
      {n_ /; l2in <= l2data[[n]]} :> {n - 1, n}, {n_} :> {n, n + 1}};
  {$l2[1], $l2[2]} = l2data[[{i2[1], i2[2]}]];
  $a[1] = ifns[[i2[1]]][l1in];
  $a[2] = ifns[[i2[2]]][l1in];
  InterpolatingPolynomial[{{{$l2[1]}, $a[1]}, {{$l2[2]}, $a[2]}}, l2in]
  ]

afn = if[sols];

Plot3D[afn[l1, l2], {l1, 0, 3.5}, {l2, 0, 3.5}]