How can Mathematica help me to find a real radical expression for roots of this polynomial?‎

Question

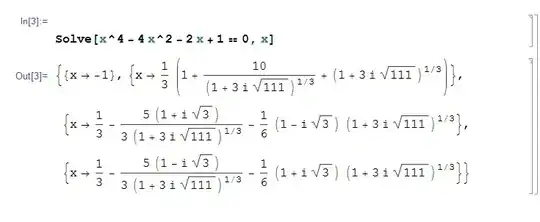
The polynomial $P(x)=x^‎‏4‏‎-‎‏4‏x^‎‏2‏‎-‎‏2‏x+‎‏1$‏‎ has ‎‏4‏‎ real roots (this can be clearly checked by plotting). But solving $P(x)=‎‏0‏‎$, using Solve[x^‎‏4‏‎-‎‏4‏x^‎‏2‏‎-‎‏2‏x+‎‏1‏‎==‎‏0‏‎,x] leads to x=-‎‏1‏‎ and ‎‏3‏‎ other roots which (however they're ‎not) seems complex number as they are represented in terms of $i$ (the imaginary unit):‎ Solve result

But I want to have the roots represented in a real closed radical expression. I mean neither in ‎trigonometric representation (such as the output of ComplexExpand[]) nor with any $i$'s in it. Is ‎there any simplification function or procedure that can help?‎ ‎ I've tried Simplify[] and FullSimplify[] and their various options. Even I've combined them with ‎some other expression manipulation functions such as Expand[], Refine[] and ComplexExpand[], ‎but I could not reach my goal.

I remember from my university days in the distant past that some real roots of certain quadric equations have no representation in terms of combinations of radicals and rational numbers. This may be such a case. — m_goldberg, Sep 08 '14 at 06:12
See Casus Irreducibilis and/or this notebook. The roots can be expressed without the imaginary unit, if you are willing to accept trig functions - just hit your output with ComplexExpand. — Mark McClure, Sep 08 '14 at 06:43
To state more strongly what other comments note: what you want cannot be done. — Daniel Lichtblau, Sep 08 '14 at 15:08

score 5 · Answer 1 · answered Sep 09 '14 at 23:17

As stated in the comments, it is not possible to get the exact roots in the desired form.
However, it is possible to get them in any arbitrary precision (100-digit precision in the following example):

Rationalize[N[Solve[x^4 - 4 x^2 - 2 x + 1 == 0, x], 100], 0]

{{x -> -1}, 
 {x -> 148845339002531569051638627576397352071169969019092/
       68589588442601901747538163421051848353066356246917}, 
 {x -> -(53523407249914715278682495786123302627314986818931/
       36135304532328057570688476882478262824336711940507)}, 
 {x -> 24375413419753596751919874615468440606916785148237/
       78350372608103708508713638007384658562420306644851}}

x^4 - 4 x^2 - 2 x + 1 /. % // N

{0., 3.3459*10^-99, 4.60681*10^-100, 1.13719*10^-100}

score 3 · Answer 2 · answered May 16 '15 at 03:52

Radicals are traditional bronze-age mathematics, but they aren't the nicest way to express the roots of a polynomial. Radical expressions are numerically unstable when a discriminant is near zero, and they often require complex arithmetic even for real results, as you've seen.

In the space age, we have Root objects, one of the real gems of Mathematica.

roots = Solve[x^4 - 4 x^2 - 2 x + 1 == 0, x, Cubics -> False]

{{x -> -1}, {x -> Root[1 - 3 #1 - #1^2 + #1^3 &, 1]}, {x -> Root[1 - 3 #1 - #1^2 + #1^3 &, 2]}, {x -> Root[1 - 3 #1 - #1^2 + #1^3 &, 3]}}

Root objects look a little peculiar, but when constructed using exact constants (as above) Mathematica treats them as exact numbers. It can, for example, tell you that the imaginary part of each root is exactly zero:

Im[x /. roots]
{0, 0, 0, 0}

When you want numerical results, Root objects are not prone to the numerical instability of radical expressions, nor will real roots contain the imaginary artifacts of incomplete cancellation.

roots // N
{{x -> -1.}, {x -> -1.48119}, {x -> 0.311108}, {x -> 2.17009}}

How can Mathematica help me to find a real radical expression for roots of this polynomial?‎

2 Answers2

Linked