The output of NDSolve is a (list of)InterpolatingFunction(s). In standard output format the elements of interpolation are not printed explicitly. I want to know if there is any way to access these values?
I need to obtain the value of the solution of an ODE system, at the endpoint of the interval, let's sayt=3. I use NDSolve as follows:

The output is a vector of InterpolatingFunctions. When I put the answers vector in Psi[t](a vector of functions of t) and then replace the variable t by 3, it seems that Mathematica starts interpolating all functions and then replaces t=3.
But for some large systems (more than 30000 x 30000). this procedure becomes unbearably time consuming or even impossible for a PC (Corei5 & 4GB of RAM) to perform. Thus, if both of the interpolating points and the corresponding values be available (at least at boundary points), they can be used instead, much more simply.
Asked
Active
Viewed 1,931 times
4
Toughee
- 113
- 5
1 Answers
5
In version 9 you can use Part to access the parts of an InterpolatingFunction:
points = {{0, 0}, {1, 1}, {2, 3}, {3, 4}, {4, 3}, {5, 0}};
ifun = Interpolation[points]
(* InterpolatingFunction[{{0,5}},<>] *)
{ifun[[3]], ifun[[4]]}
(* {{{0,1,2,3,4,5}},{{0},{1},{3},{4},{3},{0}}} *)
You can also access Properties of ifun using (not ifun["Properties"] as one would expect) ifun["Methods"]:
ifun["Methods"]
(* {"Coordinates", "DerivativeOrder", "Domain", "ElementMesh",
"Evaluate", "Grid", "InterpolationOrder", "MethodInformation",
"Methods", "Properties", "ValuesOnGrid"} *)
{ifun["Coordinates"][[1]], ifun["ValuesOnGrid"]}
(* {{0,1,2,3,4,5}, {0,1,3,4,3,0}} *)
Using the above with NDSolve
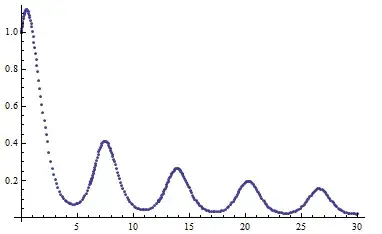
s = NDSolve[{y'[x] == y[x] Cos[x + y[x]], y[0] == 1}, y, {x, 0, 30}]
(* {{y -> InterpolatingFunction[{{0.,30.}},<>]}} *)
if1 = s[[1, All, -1]]
(* InterpolatingFunction[{{0.,30.}},<>] *)
{if1["Coordinates"][[1]], if1["ValuesOnGrid"]} // Short
(* {{0.,0.00017069,0.00034138,<<332>>,29.7515,29.8757,30.},{<<1>>}}*)
coords = Transpose[{if1["Coordinates"][[1]], if1["ValuesOnGrid"]}];
ListPlot[coords]
Related Q/As:
How to splice together several instances of InterpolatingFunction
kglr
- 394,356
- 18
- 477
- 896
s[[1,1,-1]]) this syntax happens to work fine with a single functiony. However, the correct form that works in general iss[[1,All,-1]]. It is an alternative to{x,y,z}/. s //Firstto get the right-hand-sides ofRules insides. – kglr Sep 25 '14 at 03:17ifun["Methods"]has grown to{"Coordinates", "DerivativeOrder", "Domain", "ElementMesh", "Evaluate", "GetPolynomial", "Grid", "InterpolationMethod", "InterpolationOrder", "MethodInformation", "Methods", "OutputDimensions", "Periodicity", "PlottableQ", "Properties", "QuantityUnits", "Unpack", "ValuesOnGrid"}. – bbgodfrey May 13 '18 at 13:57