Spherical parametric plot

Question

How can I plot such a parametrized curve:

$r = 2\cos t + \sin t$

$\theta = t$

$\phi = \sin 10t$

where $0<t<\pi/2$.

In the documentation only has been discussed parametric plot in Cartesian coordinates.

Answer 1

1. covert your spherical parametrized curve into cartesian parametrized curve with formulas:

$$\begin{cases} x&=r\sin\theta\cos\varphi\\ y&=r\sin\theta\sin\varphi\\ z&=r\cos\theta \end{cases}$$

in Mathematica better use some function for this:

    ConvertToCartesianParametr[r_, theta_,phi_] :=
    {r*Sin[theta]*Cos[phi], *Sin[theta]*Sin[phi], r*Cos[theta]}

2. use ParametricPlot3D as mentioned by Alexei Boulbitch

   r = 2*Cos[t] + Sin[t];
   theta = t;
   phi = Sin[10*t];
   ParametricPlot3D[ConvertToCartesianParametr[r, theta, phi], {t, 0, 2*Pi}]
   

Answer 2

If you have version 9+ you can use:

ParametricPlot3D[
   Evaluate[CoordinateTransform["Spherical" -> "Cartesian",{2 Cos[t]+Sin[t],t,Sin[10 t]}]],
    {t,0,Pi/2}]

Answer 3

It is just the answer of @kguler, with a slight modification. Try this:

    ParametricPlot3D[{(2 + Cos[t] + Sin[t])*Sin[t]*
   Cos[Sin[10 t]], (2 + Cos[t] + Sin[t])*Sin[t]*
   Sin[Sin[10 t]], (2 + Cos[t] + Sin[t])*Cos[t]}, {t, 0, 2 Pi}]

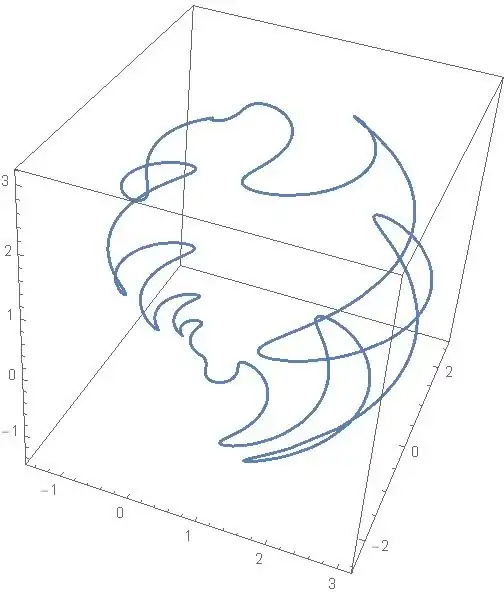
A nice curve it is. Have fun!