3

Suppose I have an image created by the code provided below. I want to select a line (1D vector) $ \left(y-y_{0}\right)=n\left(x-x_{0}\right) $ from the output image (2D matrix) by specifying $n$ and $\left(x_{0},y_{0}\right)$. Can anyone explain how to do this?

Code: 

w1 = 600;
w2 = 600;
mask = Sum[
  RotateRight[
    Exp[I k] DiskMatrix[20, {w1, w2}], {k 100, k 200 }], {k, 2}] + 
    Exp[I 5] DiskMatrix[20, {w1, w2}] + 
    Sum[RotateLeft[Exp[I k] DiskMatrix[20, {w1, w2}], {k 200, k  }], {k, 1}]
<< Developer`
Image[RotateRight[
Re[Fourier[mask]], {w1/2, w2/2}]\[TensorProduct]ToPackedArray[{1.0, 0.3, 0.1}], Magnification -> 0.4]

Mathematica graphics

Öskå
  • 8,587
  • 4
  • 30
  • 49
Asaf Miron
  • 347
  • 1
  • 9
  • The value for the variable dat is missing. I could not create any output graphics. – halirutan Oct 14 '14 at 14:57
  • Sorry about that, fixed it – Asaf Miron Oct 14 '14 at 14:59
  • By the way, you can control the brightness of the image using for example Image[10 RotateRight[... instead of Image[RotateRight[.... However, in this case the image is just being used for display purposes, and it sounds like you're interested in taking a line-shaped subset of the array Re[Fourier[mask]] itself. Is that what you're trying to do? – DumpsterDoofus Oct 14 '14 at 15:02
  • @ DumpsterDoofus Yup, that's right. And I need to be able to easily select the angle of said subset. – Asaf Miron Oct 14 '14 at 15:10

1 Answers1

3

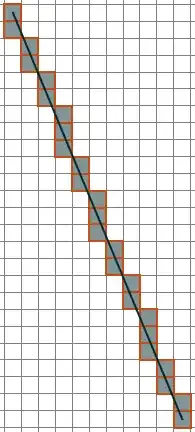
I'm sure you know that a line will almost never run through exact pixel positions. Therefore, you have two choices. First, you interpolate your image matrix and then you can sample as many points along the line as you like. In this case, I probably wouldn't recommend it because the values depend on the interpolation itself. Another, very easy way is to use an algorithm which is used draw an approximate line in a pixel grid.

Lucky for you we already had a post about his. Therefore, you can read in this answer how it is done and with the provided function, you will get the pixel coordinates along a line between points $p_0$ and $p_1$.

bresenham

bresenham[p0_, p1_] := 
 Module[{dx, dy, sx, sy, err, newp}, {dx, dy} = Abs[p1 - p0];
  {sx, sy} = Sign[p1 - p0];
  err = dx - dy;
  newp[{x_, y_}] := 
   With[{e2 = 2 err}, {If[e2 > -dy, err -= dy; x + sx, x], 
     If[e2 < dx, err += dx; y + sy, y]}];
  NestWhileList[newp, p0, # =!= p1 &, 1]]

and then you take your image and use ImageData to get the pixel matrix. The extraction of the diagonal image is as simple as

img = Import["https://i.stack.imgur.com/FQthc.png"];
Extract[ImageData[img], bresenham[{1, 1}, ImageDimensions[img]]]

Final note: pay attention that the image matrix is reversed to what you see in the image. I guess you can do the transformation of a line in two-point form and yours by yourself.

Community
  • 1
halirutan
  • 112,764
  • 7
  • 263
  • 474
  • Thanks for the help but when I try to use the code I get an error message. Any Idea why? – Asaf Miron Oct 15 '14 at 10:15
  • w1 = 600; w2 = 600; mask = Sum[RotateRight[Re[Exp[I 56 k] DiskMatrix[20, {w1, w2}]], {k 100, k 200 }], {k,2}] + Re[Exp[I 5]DiskMatrix[20, {w1, w2}]] + Sum[RotateLeft[Re[Exp[I 5 k] DiskMatrix[20, {w1, w2}]], {k 200, k }], {k, 1}]Image[0.5 mask, Magnification -> 1] << Developer ft = (Re[Fourier[mask]])^2 ift = Image[RotateRight[ft, {w1/2, w2/2}][TensorProduct]ToPackedArray[{1.0, 0.3,0.1}],Magnification -> 1] bresenham[p0_, p1_] := Module[{dx, dy, sx, sy, err, newp}, {dx, dy} = Abs[p1 - p0];{sx, sy} = Sign[p1 - p0];err = dx - dy; – Asaf Miron Oct 15 '14 at 10:17
  • @AsafMiron No, I don't know why. You have to ensure that your points $p_0$ and $p_1$ lie within your image matrix, but otherwise it's pretty fail-safe. I cannot run your code in the comment since it cropped. – halirutan Oct 15 '14 at 11:19
  • newp[{x_, y_}] := With[{e2 = 2 err}, {If[e2 > -dy, err -= dy; x + sx, x], If[e2 < dx, err += dx; y + sy, y]}]; NestWhileList[newp, p0, # =!= p1 &, 1]] Image[Extract[ImageData[ift],bresenham[{0, 0},ImageDimensions[ift]]]]` – Asaf Miron Oct 15 '14 at 11:46
  • Yeah, sorry about that. There is the remaining part. I'm very new to Mathematica and to any use of a computer to do calculations so I might be missing something simple – Asaf Miron Oct 15 '14 at 11:49
  • @AsafMiron hehe.. and without executing your code I see that you used {0,0} as starting point :-) List and matrices in Mathematica start with the index 1 – halirutan Oct 15 '14 at 12:04
  • I try to learn something new every day :). This is not the only problem I think. Did you manage to run the code? – Asaf Miron Oct 15 '14 at 12:06
  • @AsafMiron Can you join [chat] to discuss what else than a line of pixel should be the result? Because this is exactly what I get out of your code: One line of pixels. – halirutan Oct 15 '14 at 12:14
  • Just did, I'm there – Asaf Miron Oct 15 '14 at 12:20