Poincaré map for dynamic billiard

Question

There's a very nice demonstration of dynamic billiard written by Dan S. Reznik that can be found on demonstrations wolfram(along with the code): here

I was thinking whether it would be possible to draw the Poincaré map of the system for different setups (different parameters: initial angle etc), or for a whole run, meaning an animated Poincaré map (like the animated map for the kicked rotator on wiki).

The aim is to draw a Poincaré map for a run, if possible, by run I mean: as you see in the image below, you can press the "play" button for "start position angle" and see the animation.

enter image description here

Any assistance would be greatly appreciated. Thanks to Dan S. Reznik again for this beautiful piece of code.

it seems the function you want is getEllipseRefls. You should be able to extract from it the trajectory in order to build your Poincare map (?) — chris, Oct 18 '14 at 13:58
@chris yes indeed, but it runs without it, just remove the tick of "foci" (see image), and it'll be fine. — Ellie, Oct 18 '14 at 13:58
so what is it you want to slice? extract x position at y=0? For Poincare maps I know you would plot e.g. x and $\dot x$ but here it is not clear. — chris, Oct 18 '14 at 14:04
@chris well yeah a perpendicular plane passing through $x=0$ would already be a good start, because once we know how to draw the poincaré maps, then we can change these things up. I guess for our purposes we can fix the magnitude of $d\vec x / dt$ to a constant. — Ellie, Oct 18 '14 at 14:08
@Phonon I wasn't (entirely) ignoring your invitation. It looked complicated and I didn't have time yesterday. I guess chris's answer is what you were looking for, though. Generally (I thought), the first-return function (Poincaré map) is defined on a section through an initial condition that produces a periodic orbit in phase space (position-angle space in this case). I have trouble seeing that that is what chris's code produces, but the images have structure and are therefore interesting nonetheless. Cheers — Michael E2, Oct 19 '14 at 15:51
Unfortunately, I'm not familiar with the techniques of such systems that have discontinuous jumps in the velocity, nor with what is known, if anything, about Poincaré maps of them. — Michael E2, Oct 19 '14 at 17:26

chris · Accepted Answer · 2014-10-18T17:20:39.673

you could start with a simple hack of your code to extract the intersections; Something like

  {x1, y1} = Transpose[line]; 
  {x2, y2} = Transpose[RotateLeft[line]];
  gr2 = {(x1^2 - x1*x2 + y1*(-y1 + y2)), (y1 - y2)} // Transpose // Most;

which can be encapsulated in the ellipseSimLowLevel as follows

  ellipseSimLowLevel[ellPos_, θ_, aimAt_, refls_, ella_, ellb_, showFocii_] := 
  Module[{sph = Circle[{0, 0}, 1.], pt, rhat, nfact = .5, ab, 
  pr = 1.5, line, gr, fdist, focii, ellX, x1, y1, x2, y2, gr2},
  ab = {ella, ellb};
 ellX = ella*clamp[ellPos, -1, 1];
 pt = {ellX, ellipseY[ellX, ab]};
 fdist = focalRadius[ella, ellb];
 focii = 
 If[ella > 
  ellb, {{-fdist, 0}, {fdist, 0}}, {{0, -fdist}, {0, fdist}}];
 rhat = 
 Switch[aimAt, "f1", unit[focii[[1]] - pt], "f2", 
 unit[focii[[2]] - pt], _,(*-r2d[θ Degree].normEllipse[pt,
 ab]*)r2d[θ Degree].{0, -1}];
 line = getEllipseRefls[pt, rhat, ab, refls][[All, 1]];
 gr = {{Scale[sph, ab, {0, 0}]}, {Black, Line[line], 
  PointSize[Medium], Point[line]},
 {PointSize[Large], Red, Thickness[Large], 
  Arrow[{pt - nfact*rhat, pt}]},
 If[showFocii, {PointSize[Large], Blue, Point[focii]}, {}]};
 gr = Graphics[gr, Frame -> True, AspectRatio -> Automatic, 
 ImageSize -> {450, 450}, PlotRange -> {{-pr, pr}, {-pr, pr}}];
 (* NEW PART *)
{x1, y1} = Transpose[line]; 
{x2, y2} = Transpose[RotateLeft[line]];
 gr2 = {(x1^2 - x1*x2 + y1*(-y1 + y2)), (y1 - y2)} // Transpose // Most;
 gr2 = Graphics[Map[Point, gr2], Frame -> True, AspectRatio -> 1, 
 ImageSize -> {450, 450}];
 Row@{gr, gr2}
 (* END OF NEW PART *)
 ];

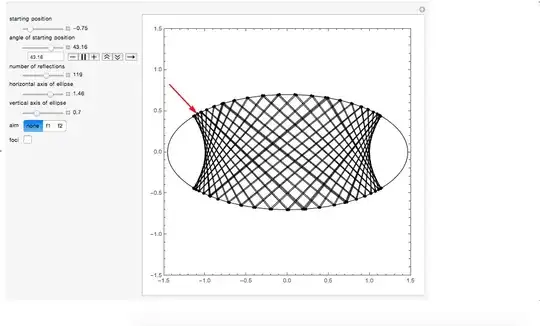
Then the above Manipulate produces

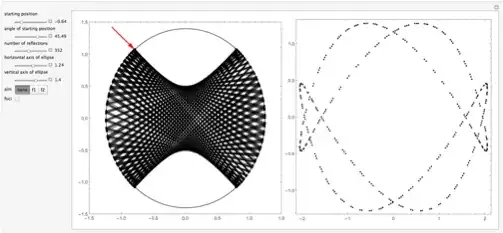
Mathematica graphics

or

Mathematica graphics

or

Mathematica graphics

Okay, is there a way to put a manipulate bar next to the others, that would allow to change the coordinates through which the plane of intersection with phase space passes? sounds unlikely, thought I'd ask :( — Ellie, Oct 18 '14 at 15:53
sure: you just have to find the intersections of the lines with your plane... — chris, Oct 18 '14 at 16:42

Poincaré map for dynamic billiard

1 Answers1

Linked