Plotting two recursive functions

Question

I'm trying to plot two recursive functions (p and θ) on a map. So far I have:

θ0 = Pi/2;
p0 = 0;
α = 0.1;
β = 1;

θ[j_] := θ[j] = θ[j - 1] + β*p[j - 1];
p[j_] := p[j] = 
   p[j - 1] - α*Sin[θ[j - 1] + β*p[j - 1]];
θ[0] = θ0;
p[0] = p0;

How can I plot p[j] against θ[j] for 0 <= j <= 100?

Mr.Wizard · Accepted Answer · 2014-10-18T23:06:06.657

6

I think you are looking for DiscretePlot:

DiscretePlot[{θ[j], p[j]}, {j, 0, 100}]

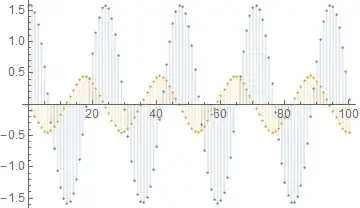
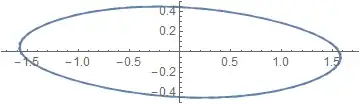
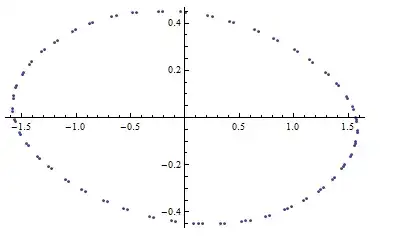
enter image description here

Or perhaps you want something like this?:

ListPlot @ Table[{θ[j], p[j]}, {j, 0, 100}]

enter image description here

Another method is to use ParametricPlot after sufficiently coercing the input, e.g.:

f[x_?NumericQ] := {θ[#], p[#]} & @ Round @ x

ParametricPlot[f[j], {j, 0, 100}]

enter image description here

(Aspect ratio may be controlled with the AspectRatio option.)

edited Oct 18 '14 at 23:06

answered Oct 18 '14 at 22:38

Mr.Wizard

271,378
34
587
1,371

that plots p and θ by j. I need to plot p by θ (for every matching j) as it if were a phase space – Geo Oct 18 '14 at 22:39
@Geo You mean you want p on one axis and θ on the other? – Mr.Wizard Oct 18 '14 at 22:41
yeah. sorry my not being so clear on the question. – Geo Oct 18 '14 at 22:43
@Geo Please see update. – Mr.Wizard Oct 18 '14 at 22:43
ahh that's it. Thank you sir. – Geo Oct 18 '14 at 22:44
@Geo You're welcome. One point: you said "for every matching j" but all points match. Do you have a case where they do not? You may need to filter the result of Table using e.g. Cases or Select. Let me know if you need help. – Mr.Wizard Oct 18 '14 at 22:50
ehh english not my mother language. What I meant was (p1,θ1), (p2,θ2) and so on. what you did is completely correct. In case I have any trouble I will let you know. Thanks – Geo Oct 18 '14 at 23:04
@Geo Okay, no problem. I added another method for your interest. – Mr.Wizard Oct 18 '14 at 23:08

score 3 · Answer 2 · edited Oct 19 '14 at 02:26

3

A proposal using Functional paradigm to avoid recursive functions.

data=
 With[{α = .1, β = 1},
   NestList[
    {#[[1]] + β #[[2]], #[[2]] - α Sin[#[[1]] + β #[[2]]]} &,
    {Pi/2, 0}, 100]];

ListPlot[data]

edited Oct 19 '14 at 02:26

Mr.Wizard

271,378
34
587
1,371

answered Oct 19 '14 at 02:25

xyz

605
4
38
117

2

Although this doesn't directly answer the question it does show a good technique; NestList is often faster and simpler than recursion in Mathematica. By the way this can also be written: With[{α = .1, β = 1}, NestList[{# + β #2, #2 - α Sin[# + β #2]} & @@ # &, {Pi/2, 0}, 100]] – Mr.Wizard Oct 19 '14 at 02:29
@Mr.Wizard,+1, your solution is indeed I need! I am alway writing the code: With[{α = .1, β = 1}, NestList[{# + β #2, #2 - α Sin[# + β #2]} & , [Pi/2, 0], 100]] before. Thanks sir! – xyz Oct 19 '14 at 02:32
2

You're welcome. Another method you might like: With[{α = .1, β = 1}, NestList[# /. {x_, y_} :> {x + β y, y - α Sin[x + β y]} &, {Pi/2, 0}, 100]] as described here: (8399). This can be more readable than an excessive number of #* parameters. – Mr.Wizard Oct 19 '14 at 02:50
that's interesting. I will try using this for plotting the results for different initial conditions on the same graph. thanks – Geo Oct 20 '14 at 12:43
@Geo,see here，my answer is at last. – xyz Oct 20 '14 at 13:15

Plotting two recursive functions

2 Answers2

Linked

Related