13

I was curious about the difference in speed between Total and Sum. I found out Total was faster. However on another occasion I used a longer list and then the result was reversed. Upon closer inspection, I saw that Sum behaved strangely, see the repetitive code below:

Sum[x, {x, 1, 10^4}] // AbsoluteTiming
Sum[x, {x, 1, 10^5}] // AbsoluteTiming
Sum[x, {x, 1, 10^6}] // AbsoluteTiming
Sum[x, {x, 1, 10^7}] // AbsoluteTiming
Sum[x, {x, 1, 10^8}] // AbsoluteTiming
Sum[x, {x, 1, 10^9}] // AbsoluteTiming

{0.000377, 50005000}

{0.002676, 5000050000}

{0.162434, 500000500000}

{0.000157, 50000005000000}

{0.000112, 5000000050000000}

{0.000110, 500000000500000000}

I can not make any sense of the results above.

Compare those with the more expected results from Total

Total[Range[10^4]] // AbsoluteTiming
Total[Range[10^5]] // AbsoluteTiming
Total[Range[10^6]] // AbsoluteTiming
Total[Range[10^7]] // AbsoluteTiming
Total[Range[10^8]] // AbsoluteTiming
Total[Range[10^9]] // AbsoluteTiming

{0.000115, 50005000}

{0.000931, 5000050000}

{0.010395, 500000500000}

{0.101801, 50000005000000}

{1.166246, 5000000050000000}

{12.470277, 500000000500000000}

Can anyone explain what causes this strange behavior ?

MathLind
  • 1,697
  • 1
  • 13
  • 22
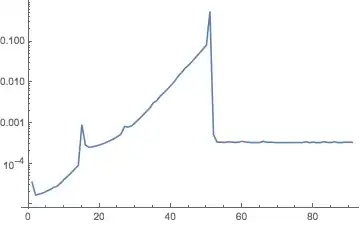
  • Total will most surely sum blindly, while Sum[] could use known properties (at least it will try when n is large enough) – Dr. belisarius Nov 04 '14 at 19:45
  • For simple problems do the sum symbolically. sum[n_Integer?Positive] = Sum[x, {x, 1, n}] – Bob Hanlon Nov 04 '14 at 19:58
  • @belisarius - so you mean, Sum's algorithm changes when the list reaches a certain length? – MathLind Nov 04 '14 at 20:06
  • @MathLind Well, I can't be sure, but it won't surprise me if it does – Dr. belisarius Nov 04 '14 at 20:08
  • 2
    "If a sum cannot be carried out explicitly by adding up a finite number of terms, Sum will attempt to find a symbolic result. In this case, f is first evaluated symbolically." Presumably, "cannot be carried out explicitly" translates approximately to more than 10^6 terms. – Bob Hanlon Nov 04 '14 at 20:15
  • I did your Sums on my Mathematica in a different order and got qualitatively different results. The 10^6 took a lot longer, but the 10^7 took even longer. Then, 10^8 was very quick. When using Mathematica for timing, be sure to clear caches/etc to make sure you're not getting inaccurate times. Restarting Mathematica each time might also make the timing more accurate. –  Nov 04 '14 at 20:54
  • Doesn't Mathematica know that this sum is n(n+1)/2? – John McGee Nov 04 '14 at 21:59
  • @JohnMcGee: Yes, when it is input as an indefinite sum, or when the summation bounds are symbolic. When it is given a numeric range, it looks like it just adds up the numbers manually. See my answer for an illustration of this behavior. – DumpsterDoofus Nov 04 '14 at 22:11

3 Answers3

12

Sum uses more than one Method. By default it selects automatically. If you specify one of them you should see more consistent behavior:

SetOptions[Sum, Method -> "Procedural"];

Table[
  Sum[x, {x, 1, 10^n}] // AbsoluteTiming,
  {n, 4, 9}
] // MatrixForm

$\left( \begin{array}{cc} 0.001000 & 50005000 \\ 0.003000 & 5000050000 \\ 0.011001 & 500000500000 \\ 0.104006 & 50000005000000 \\ 0.768044 & 5000000050000000 \\ 10.313590 & 500000000500000000 \\ \end{array} \right)$

Symbolic summation:

SetOptions[Sum, Method -> "RationalFunction"];

Table[
  Sum[x, {x, 1, 10^n}] // AbsoluteTiming,
  {n, 4, 9}
] // MatrixForm

$\left( \begin{array}{cc} 0.002000 & 50005000 \\ 0.002000 & 5000050000 \\ 0.001000 & 500000500000 \\ 0.002000 & 50000005000000 \\ 0.002000 & 5000000050000000 \\ 0.001000 & 500000000500000000 \\ \end{array} \right)$

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • Thank you for a clear answer. I still find it peculiar that Sum is optimized in such a way as to give rise to a 1000-fold speed jump at a certain list length. What I mean by that is, what it apparently needs roughly 10^7 of list length to realize, it should have detected earlier in shorter lists. – MathLind Nov 05 '14 at 20:46
  • 3
    @MathLind Thanks for the Accept. I think it is a matter of Mathematica not knowing in advance which method will be fastest. Even the "slow" attempt takes under a fifth of a second. You can let Mathematica try multiple methods in parallel by using Method -> "ParallelFirstToSucceed" but I think you will find that the overhead of that is often slower than the default behavior. Perhaps this could be better optimized but there are other aspects of Mathematica that I consider in far greater need of optimization; specifically the pattern matching. – Mr.Wizard Nov 05 '14 at 23:41
  • @ Mr.Wizard For me this was an awakening in the context of optimizing code (programs) containing many built-in functions that behave in this way. Without profiling tools, this may possibly require laborious and careful parameter study of all the built-in functions within the expected ranges. A challenge but still very interesting. – MathLind Nov 06 '14 at 08:22
  • @MathLind Indeed Mathematica can be fiddly that way. There is a profiling tool built in, detailed here: (7768). It has a few quirks but it seems to work acceptably accurately. – Mr.Wizard Nov 06 '14 at 08:27
8

The pattern becomes more obvious when plotted:

ListLogPlot[
 Table[First@AbsoluteTiming@Sum[x, {x, 1, Round[10^k]}], {k, 1, 10, 
   0.1}], PlotRange -> All, Joined -> True]

enter image description here

This appears to be consistent with Bob Hanlon's observation that Sum attempts to explicitly sum when the number of terms is considered tractable (the time expense of which is linear), and then search for general solutions after that and use bound substitution (which is fast, and proceeds in constant time). Mr. Wizard's answer provides more details.

DumpsterDoofus
  • 11,857
  • 1
  • 29
  • 49
1

This seems like an area where Mathematica can be improved. Mathematica knows the general sum with increment of 1. Applying it is very fast.

In[1]  sn = Sum[x, {x, a, b}]
Out[1] -(1/2) (a-b-1) (a+b)
In[2 ] sn /. {a -> 1, b -> 10^35} // AbsoluteTiming
Out[2] {0.,5000000000000000000000000000000000050000000000000000000000000000000000}

We could define a function for this

FastSum[x_, {x_, a_, b_}] := 1/2 (b - a + 1) (a + b);
John McGee
  • 2,538
  • 11
  • 15