0

There is an interesting discussion on performance of Sum[] in this question.

I actually wanted to reproduce findings from this answer.

So, I entered:

ListLogPlot[
 Table[First@AbsoluteTiming@Sum[x, {x, 1, Round[10^k]}], {k, 1, 10, 
   0.1}], PlotRange -> All, Joined -> True]

and got:

enter image description here

which is somewhat different from the graph from the answer that I linked to above:

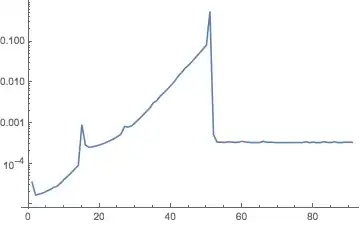
enter image description here

(I don't mean trivial differences like y-axis scale, etc; I mean qualitative differences, like absence or presence of smaller spikes, relation between values for 30, 40, 50)

What happens on your machine? Why the difference?

Community
  • 1
Adrian
  • 411
  • 4
  • 14
  • Win 7, 2GB, Celeron T3500 2.1GHz is my machine basic spec. – Adrian Nov 13 '14 at 14:24
  • I would guess that the resolution of AbsoluteTiming is system dependent. For example, on my Win 7 PC, I never get a value between 0 and 0.0005, so that's probably the resolution of some clock that AbsoluteTiming uses. If you compare only timings large compared to the clock resolution (e.g. t > 0.01), the graphs do look very similar. – Niki Estner Nov 13 '14 at 14:34
  • The scale matters. If you account for it then all the stuff stat "looks" different, prior to 40 or so, is really not relevant. – Daniel Lichtblau Nov 13 '14 at 15:07
  • @Adrian Hey :) I was wondering why do you spend so much time editing old posts when you can try to improve new ones, ones that do not have an answer yet. It's kinda pointless to improve a post from years ago when it has 20+ votes, 3+ answers and you only re-tag it ... – Sektor Nov 21 '14 at 14:44

0 Answers0