Question in ParametricPlot3D, how to join the minima of a {x,y} function

Question

Thanks to my previous question I have plotted the function with the following code:

a[x_, y_] := (x^2 - 3 - 9*y)^2 + 50*y^2
ParametricPlot3D[{x, #, a[x, #]} & /@ {0, 2, 4, 6, 8, 10, 12}, {x, -13, 13}, 
  BoxRatios -> 1, ImageSize -> 350, Boxed -> False]

Now I want to join the minima. How should I proceed?

kglr · Accepted Answer · 2014-11-13T15:15:53.273

a[x_, y_] := (x^2 - 3 - 9*y)^2 + 50*y^2

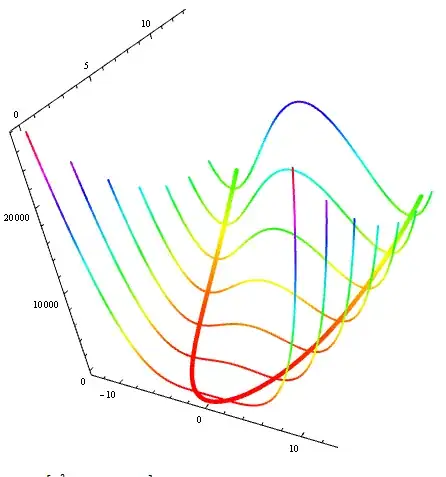
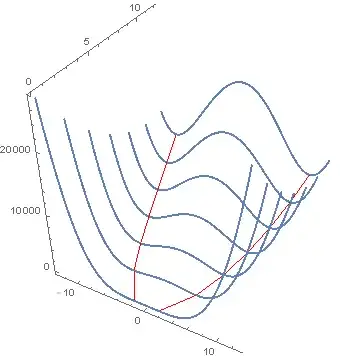
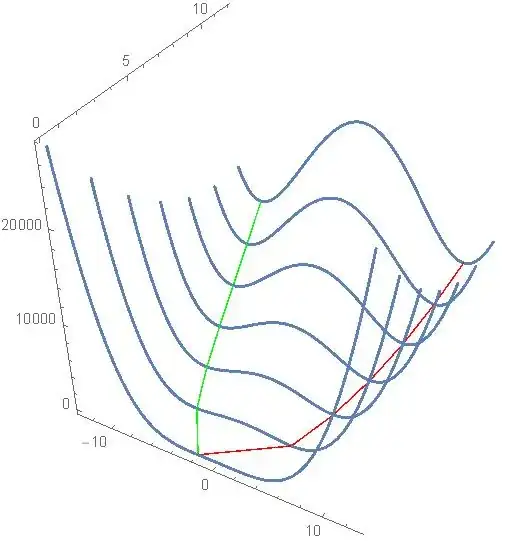
Plot3D with MeshFunctions

Using a single Plot3D with multiple MeshFunctions:

Plot3D[a[x, y], {x, -13, 13}, {y, -.001, 12.1},
 PlotStyle -> Opacity[.5], BoundaryStyle -> None, Boxed -> False, BoxRatios -> 1,
 MeshFunctions -> {#2 &, 
          ConditionalExpression[Derivative[1, 0][a][#, #2], Derivative[2, 0][a][#, #2] > 0] &}, 
 Mesh -> {{0, 2, 4, 6, 8, 10, 12}, {0}},
 MeshStyle -> Dynamic@{Directive[{Thick, Hue[RandomReal[]]}],
    {Directive[{Gray, Thick}], Directive[{Gray, Thick}]}} ]

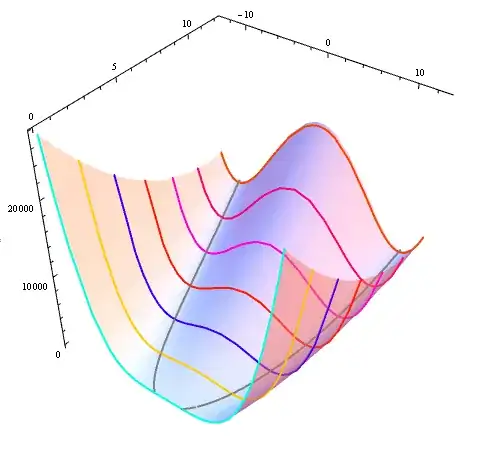
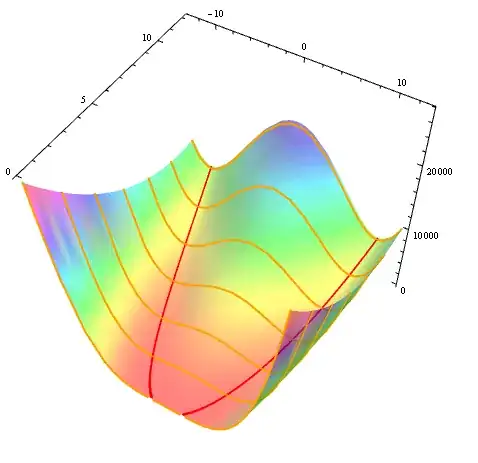
enter image description here

Plot3D with Exclusions:

Plot3D[a[x, y], {x, -13, 13}, {y, -.001, 12.1}, Boxed -> False, BoxRatios -> 1, 
 Exclusions -> {ConditionalExpression[Derivative[1, 0][a][x, y], 
                Derivative[2, 0][a][x, y] > 0]},
 ExclusionsStyle -> Red, ColorFunction -> Hue,
 PlotStyle -> Opacity[.5], BoundaryStyle -> None, 
 MeshFunctions -> {#2 &}, Mesh -> {{0, 2, 4, 6, 8, 10, 12}},
 MeshStyle -> {Directive[{Thick, Hue[RandomReal[]]}]} ]

enter image description here

ParametricPlot3D

soln = y /. Assuming[{x > -1/3},
    FullSimplify[Solve[{ConditionalExpression[Derivative[1, 0][a][y, x],
          Derivative[2, 0][a][y, x] > 0] == 0, x > -1/3}, y]]];

$\left\{-\sqrt{9 x+3},\sqrt{9 x+3}\right\}$

b[x_] := {#, x, a[#, x]} & /@ soln

{ $\left\{-\sqrt{9 x+3},x,50 x^2\right\}$, $ \left\{\sqrt{9 x+3},x,50 x^2\right\} $}

ParametricPlot3D[{b[x], {x, #, a[x, #]} & /@ {0, 2, 4, 6, 8, 10, 12}},
 {x, -13, 13},  PlotStyle -> {Thickness[.01], Thick},
 ColorFunction -> Hue, Boxed -> False, BoxRatios -> 1]

enter image description here

score 7 · Answer 2 · 2014-11-13T09:24:11.390

Because the local minima in $x$ are the zeros of the $x$-derivative, you could do something like this:

Plot3D[a[x, y], {x, -13, 13}, {y, 0, 12}, 
 MeshFunctions -> {Derivative[1, 0][a]}, Mesh -> {{0}}]

enter image description here

This also includes the local maxima, but you can get rid of them by requiring the second derivative in $x$ to be positive. Then we remove the surface itself, and we have the lines you want:

Plot3D[a[x, y], {x, -13, 13}, {y, 0, 12}, 
 MeshFunctions -> {Derivative[1, 0][a]}, Mesh -> {{0}}, 
 RegionFunction -> (Derivative[2, 0][a][##] > 0 &),
 PlotStyle -> None, BoundaryStyle -> None]

enter image description here

Use Show to put it together with the original plot.

enter image description here

The nice thing is that it still works when minima can appear and disappear:

Show[Plot3D[a[x, y], {x, -13, 13}, {y, -6, 12}, Mesh -> None, 
  BoxRatios -> 1, PlotStyle -> Opacity[0.6]], 
 Plot3D[a[x, y], {x, -13, 13}, {y, -6, 12}, 
  MeshFunctions -> {Derivative[1, 0][a]}, Mesh -> {{0}}, 
  RegionFunction -> (Derivative[2, 0][a][#1, #2] > 0 &), 
  PlotStyle -> None, BoundaryStyle -> None, ClippingStyle -> None]]

enter image description here

score 4 · Answer 3 · answered Nov 13 '14 at 08:34

You can determine the minima with

pts = Transpose[Module[{yy = #, sol1, sol2},
     sol1 = FindMinimum[a[x, yy], {x, -13}];
     sol2 = FindMinimum[a[x, yy], {x, 13}];
     {{sol1[[2, 1, 2]], yy, sol1[[1]]}, {sol2[[2, 1, 2]], yy, 
       sol2[[1]]}}
     ] & /@ {0, 2, 4, 6, 8, 10, 12}]

and then show them together with your original plot

    Show[ParametricPlot3D[{x, #, a[x, #]} & /@ {0, 2, 4, 6, 8, 10, 12}, {x, -13, 13}, 
          BoxRatios -> 1, ImageSize -> 350, Boxed -> False], 
         Graphics3D[{Red, Line[pts[[1]]]}], 
         Graphics3D[{Red, Line[pts[[2]]]}]
        ]

enter image description here

score 4 · Answer 4 · answered Nov 13 '14 at 08:42

If I got you right, you want to plot two lines going through the minimums. If yes, try the following:

This makes the lists of the points of minimums:

 a[x_, y_] := (x^2 - 3 - 9*y)^2 + 50*y^2 ;
lstA = (NMinimize[{a[x, #], x < 11}, x] & /@ {0, 2, 4, 6, 8, 10, 
      12}) /. {c_, {Rule[a_, b_]}} -> {b, c};
lstB = (NMinimize[{a[x, #], x > -11 && x <= 0}, x] & /@ {0, 2, 4, 6, 
      8, 10, 12}) /. {c_, {Rule[a_, b_]}} -> {b, c};
lst3A = Transpose[{Transpose[lstA][[1]], {0, 2, 4, 6, 8, 10, 12}, 
    Transpose[lstA][[2]]}];
lst3B = Transpose[{Transpose[lstB][[1]], {0, 2, 4, 6, 8, 10, 12}, 
    Transpose[lstB][[2]]}];

and this makes a plot:

    Show[{

  ParametricPlot3D[{x, #, a[x, #]} & /@ {0, 2, 4, 6, 8, 10, 
     12}, {x, -13, 13}, BoxRatios -> 1, ImageSize -> 350, 
   Boxed -> False],
  Graphics3D[{Red, Thickness[0.003], Line[lst3A], Green, 
    Thickness[0.003], Line[lst3B]}]

  }]

which is shown below:

enter image description here

Have fun!

Question in ParametricPlot3D, how to join the minima of a {x,y} function

4 Answers4

Linked