How to use ParametricPlot and fill closed areas with blue and red?

Question

The current code is :

ParametricPlot[{
  {Cos[t] + 1/2, Sin[t]}*10,
  5 {Cos[t/2], Sin[t/2]},
  5 {Cos[t/2 + Pi] + 2, Sin[Pi + t/2]},
  If[r < 1.1, r {Cos[t] + 10/r, Sin[t]}],
  If[r > .9 && r < 2.1, (r - 1) {Cos[t], Sin[t]}]
  },
 {t, -0.1, 2 Pi + 0.1}, {r, 0, 5}, MeshFunctions -> {#4 &}, 
 Mesh -> {{0, 1, 5}}, MeshShading -> {Red, Blue}, PlotRange -> All, 
 Frame -> {False, False}, Axes -> None, PlotStyle -> {Red, Red, Red}]

and its output:

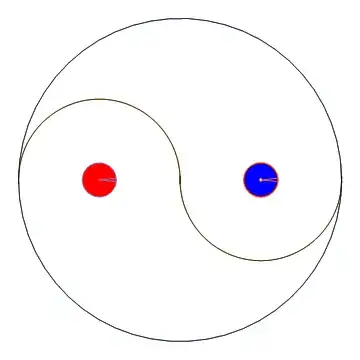
How to fill the close areas with blue neighbored by red?

Update 1 : I want to see whether it is possible to create such figure by using ParametricPlot and the region filling options.

Update 2

Desired result should be similar to:

Obtained by:

Graphics[{Red, Disk[], Blue, 
  Polygon[Join[Table[{Cos[a], Sin[a]}, {a, Pi, 2 Pi, Pi/360}], 
    Table[{-1/2, 0} + {Cos[a], Sin[a]} /2, {a, 0, Pi, Pi/360}], 
    Table[{1/2, 0} + {Cos[a], Sin[a]} /2, {a, Pi, 2 Pi, Pi/360}]]], 
  Blue, Disk[{+1/2, 0}, 1/8], Red, Disk[{-1/2, 0}, 1/8]}, 
 ImageSize -> Large]

Another similar but undesired implementation is:

Plot[{Sqrt[1 - x^2], -Sqrt[1 - x^2], Sqrt[x - x^2], -Sqrt[-x - x^2], 
  Sqrt[0.025 - (x - 0.5)^2], -Sqrt[0.025 - (x - 0.5)^2], 
  Sqrt[0.025 - (x + 0.5)^2], -Sqrt[0.025 - (x + 0.5)^2]}, {x, -1, 1}, 
 Filling -> {1 -> {Axis, Red}, 2 -> {{4}, Blue}, 2 -> {Axis, Blue}, 
   3 -> {Axis, Blue}, 4 -> {Axis, Red}, 5 -> {{6}, Red}, 
   7 -> {{8}, Blue}}, AspectRatio -> Automatic, Axes -> False, 
 PlotStyle -> None, 
 ImageSize -> Large]

which gives:

Update 3

Inspired by ubpdqn's answer below, I tried the following code:

ParametricPlot[{u {-Sin[t], Cos[t]}, u {Sin[t], Cos[t]}}, {t, 0, 
  Pi}, {u, 0, 1},
 MeshFunctions -> {(Boole[(
       If[#1 <= 0,
        #2 - Sqrt[0.25 - (#1 + 0.5)^2] >= 0 || (#1 + .5)^2 + #2^2 < 
          1/64,
        #2 + Sqrt[0.25 - (#1 - 0.5)^2] >= 0 && (#1 - .5)^2 + #2^2 > 
          1/64]
       )] &)}, Mesh -> {{0.1}}, MeshShading -> {Blue, Red}, 
 PlotPoints -> 70,
 Frame -> False, Axes -> False, BoundaryStyle -> None, 
 ImageSize -> Large]

which gives:

and should be the right answer.

Answer 1

p1[t_] := {Cos[t], Sin[t]}
p2[t_] := 0.5 {Cos[t + Pi], Sin[t + Pi]} + {0.5, 0}
p3[t_] := 0.5 {Cos[t], Sin[t]} - {0.5, 0}
p4[t_] := {Cos[t + Pi],Sin[t+Pi]}
Graphics[{{Blue, 
   Polygon[Join @@ 
     Transpose[
      Table[{p1[Pi - j], p3[j], p2[Pi-j]}, {j, 0, Pi, 0.001}]]]}, {Red, 
   Polygon[Join @@ 
     Transpose[Table[{p2[j], p3[j], p4[j]}, {j, 0, Pi, 0.001}]]]}}]

UPDATE

Automating:

fun[t_] := 
 Boole[0 <= t < Pi] p1[Pi - t] + 
  Boole[Pi < t < 3 Pi/2] p2[2 (Pi/2 - t)] + 
  Boole[3 Pi/2 < t <= 2 Pi] p3[2 (t - Pi/2)]
g[t_] := Boole[0 <= t < Pi] p4[t] + 
  Boole[Pi < t < 3 Pi/2] p2[2 (Pi/2 - t)] + 
  Boole[3 Pi/2 < t <= 2 Pi] p3[2 (t - Pi/2)]

Visualizing to achieve desired aim:

Graphics[{{Blue, Polygon[Table[fun[j], {j, 0, 2 Pi, 0.01}]]}, {Red, 
   Polygon[Table[g[j], {j, 0, 2 Pi, 0.01}]]}, {Red, 
   Disk[{0.5, 0}, 0.125]}, {Blue, Disk[{-0.5, 0}, 0.125]}}]

Answer 2

I post this is a separate answer. It uses ParametricPlot as per question title (rather than polygon). If this is against protocol, let me know and I can merge. Further, advice re: removal of vertical line(x=0&&y>0) welcome.

plt1 = ParametricPlot[u {Sin[t], Cos[t]}, {t, 0, Pi}, {u, 0, 1}, 
   MeshFunctions -> {(Boole[#1 #2 <= 0] ((#1 - 0.5)^2 + #2^2) &)}, 
   Mesh -> {{0.25}}, MeshShading -> {Blue, Red}, 
   Frame -> False, Axes -> False, BoundaryStyle -> None];
plt2 = ParametricPlot[u {-Sin[t], Cos[t]}, {t, 0, Pi}, {u, 0, 1}, 
   MeshFunctions -> {(Boole[#1 #2 <= 0] ((#1 + 0.5)^2 + #2^2) &)}, 
   Mesh -> {{0.25}}, MeshShading -> {Red, Blue}, Frame -> False, 
   Axes -> False, BoundaryStyle -> None];
Show[plt1, plt2, PlotRange -> All, 
 Epilog -> {{Red, Disk[{0.5, 0}, 0.125]}, {Blue, 
    Disk[{-0.5, 0}, 0.125]}}]