I am interested in the following implicit curve with parametric equation:
$$ \left\{\quad \begin{array}{rl} x=& 9 \sin 2 t+5 \sin 3 t \\ y=& 9 \cos 2 t-5 \cos 3 t \\ \end{array} \right. $$
ParametricPlot code:
ParametricPlot[
u {9 Sin[2 t] + 5 Sin[3 t], 9 Cos[2 t] - 5 Cos[3 t]}, {t, 0,
2 Pi}, {u, 0, 1}, MeshFunctions -> {Sqrt@(#1^2 + #2^2) &},
Mesh -> {{1}}, PlotPoints -> 30, MeshStyle -> Cyan,
MeshShading -> {Cyan}, PlotStyle -> Cyan]
produces:

How can I remove those lines inside the closed region? or at least let it be the same color as the filled color?
Additionally, for a given point $P=(x_0,y_0)$, how to determine by Mathematica whether $P$ is inside the filled region or not?
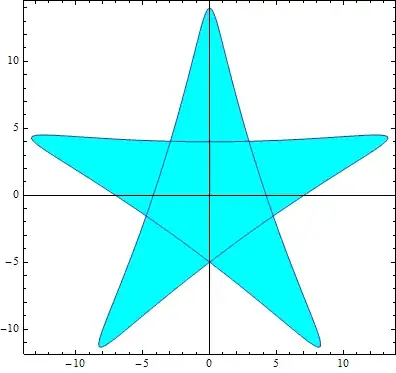

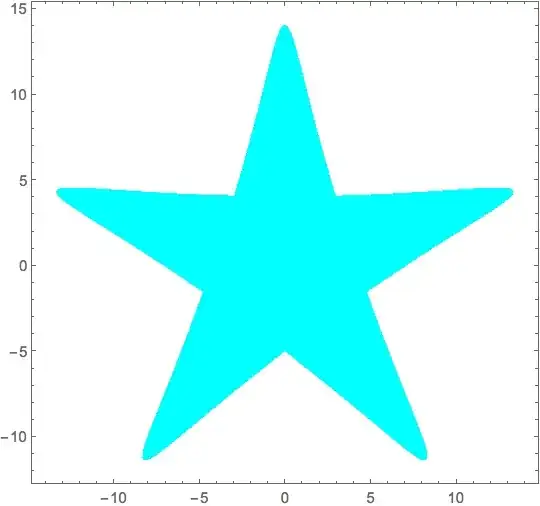
InPolygonQconsideres the inner hexagon region to be outside.. – george2079 Jun 02 '15 at 15:11InPolygonQwith another function from the linked Q/A. – kglr Jun 02 '15 at 15:45