With[{f = # + 1/# &, center = 1/3 + 3 I/2, radius = 4/3},ParametricPlot[Through[{Re, Im}[f[center + r Exp[I \[Theta]]]]], {r, 0, radius}, {\[Theta], -\[Pi], \[Pi]}, PlotPoints -> 30, PlotRange -> All, MaxRecursion -> 3]]
in Version 9,the output is:

but in Version 10:
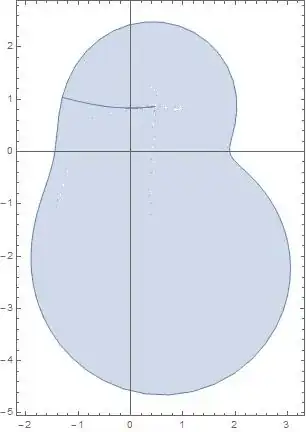
Is it a bug in Version 10?
the code links here.



PlotTheme -> "Classic"has been given in Szabolc's answer to Will Version 9 functions all work in Version 10? – Michael E2 Dec 11 '14 at 18:32