Cut a polygon by a line

Question

I have a polygon, says, Polygon[{0,0},{10,0},{10,10}{0,10}]. I would like to cut it by a line (through two points) and take one half of it. Could you please suggest me the functions I should use? (I am very new to Mathematica).

a general line that goes through 2 points. Thus the line may or may not cut the polygon — N.T.C, Dec 12 '14 at 06:26
Take a look at this http://mathematica.stackexchange.com/questions/66152/how-to-check-if-a-line-segment-intersects-with-a-polygon — Dr. belisarius, Dec 12 '14 at 06:30

score 8 · Accepted Answer · answered Dec 12 '14 at 08:42

8

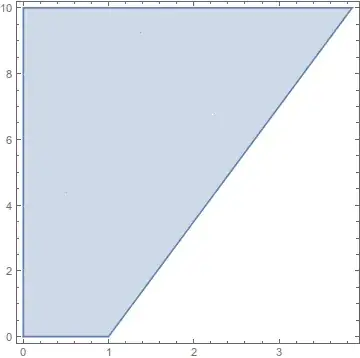
I guess a pretty easy approach is to use HalfPlane with your two points that define your line. RegionDifference should do the rest.

RegionDifference[ 
 Polygon[{{0, 0}, {10, 0}, {10, 10}, {0, 10}}], 
 HalfPlane[{{1, 0}, {3, 7}}, {1, 1}]];
RegionPlot[%]

Mathematica graphics

answered Dec 12 '14 at 08:42

halirutan

112,764
7
263
474

+1. RegionMember[reg][{x, y}] gives an algebraic representation of the region, which might be useful in certain cases. I can't immediately see an easy way to get a Polygon. BoundaryDiscretizeRegion[reg]["BoundaryPolygons"] is unsatisfying. – Michael E2 Dec 12 '14 at 13:37
that's a simple awesome answer - thank you – N.T.C Dec 17 '14 at 04:11

score 2 · Answer 2 · answered Dec 12 '14 at 06:29

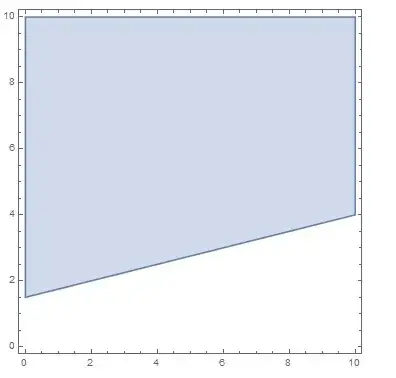
in MMA v10 (although it is slow) you can use:

Clear[r];
r[point1_, point2_] := 
 ImplicitRegion[{x, y} \[Element] 
    Polygon[{{0, 0}, {10, 0}, {10, 10}, {0, 10}}] && 
   y >= point2[[2]] + (point2[[2]] - point1[[2]])/(
      point2[[1]] - point1[[1]]) (x - point2[[1]]), {x, y}]

RegionPlot[r[{2, 2}, {6, 3}]]

enter image description here

score 2 · Answer 3 · edited Apr 13 '17 at 12:56

It seems to me there are a few sorts of answers to the question, like

a numeric visualization, e.g. a RegionPlot
a system of algebraic conditions,
a geometric one, i.e. the resulting polygon(s)

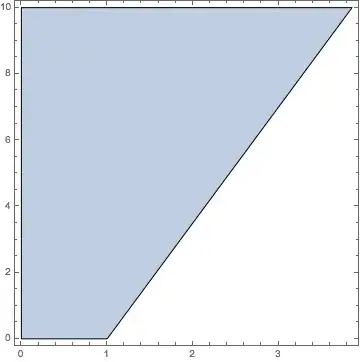
Here is a variation on halirutan's use of the geometric computation functionality:

reg = RegionIntersection[
   Polygon[{{0, 0}, {10, 0}, {10, 10}, {0, 10}}], 
   HalfPlane[{{1, 0}, {3, 7}}, -{1, 1}]];

It is easy to plot with RegionPlot[reg] and to get an algebraic system with RegionMember[reg][{x, y}], but some programming seems necessary to get a geometric solution in elementary terms.

The algebraic system is

RegionMember[reg][{x, y}]
(*
  (x | y) ∈ Reals && -7 + 7 x - 2 y <= 0 && 
   10 y >= 0 && -10 (-10 + x) >= 0 && -10 (-10 + y) >= 0 && 10 x >= 0
*)

We can find boundary polygons of the region by discretizing the region. Unfortunately, the breaks the edges into smaller line segments. These can be eliminated by removing points of the polygon that are collinear with its adjacent points.

noncollinear[m : {p1_, p2_, p3_}] := 
  MatrixRank[Transpose[m]~Append~{1., 1., 1.}, Tolerance -> 0.00001] == 3;

polys = BoundaryDiscretizeRegion[reg]["BoundaryPolygons"] /. 
  Polygon[pts_] :> Polygon[Pick[pts, noncollinear /@ RotateRight@Partition[pts, 3, 1, 1]]]
Graphics[{EdgeForm[Opacity[1]], Opacity[0.4], ColorData[97, 1], polys},
  Frame -> True, AspectRatio -> 1]
(*
  {Polygon[{{1.14952*10^-7, 2.98023*10^-7}, {1., 2.98023*10^-7},
            {3.85714, 10.}, {1.14952*10^-7, 10.}}]}
*)

Mathematica graphics

Cut a polygon by a line

3 Answers3

Linked

Related