Fullsimplify does not simplify Abs'[1.-a]

Question

I have to simplyfy an expression involving Abs' This works:

FullSimplify[Abs'[1 - a], a ∈ Reals]

Sign[1 - a]

but this does not:

FullSimplify[Abs'[1. - a], a ∈ Reals]

Derivative[1][Abs][1. - a]

the problem seems to be the 1., how can i get around this ?

Answer 1

Mathematica does not have a rule for the derivative of Abs. Assuming that the term arose from taking the derivative with respect to a then taking the derivative of Abs[1-a] results in

D[Abs[1 - a], a]

-Derivative[1][Abs][1 - a]

which would recurse forever if it evaluated. Note

Plot[{Abs[1 - a], -Sign[1 - a]}, {a, -5, 5},
 PlotLegends -> "Expressions"]

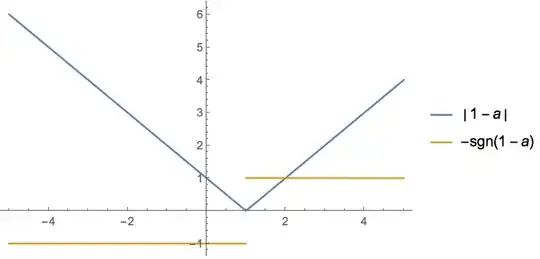
Graphically, the derivative is -Sign[1 - a] except when a == 1

If dealing with real functions, before taking the derivative of a function containing Abs the function should have the terms with Abs converted to the Sqrt of the square of the argument to Abs.

Simplify[D[Sqrt[(1 - a)^2], a], Element[a, Reals]]

Piecewise[{{-1, a < 1}}, 1]

Simplify[% == -Sign[1 - a], a != 1]

True

Answer 2

If you want to incorporate the realness assumption directly into the evaluation of the derivative, you can define it for all subsequent computations by setting

Derivative[1][Abs][x_] := Sign[x]

Abs'[1. - a]

(* ==> Sign[1. - a] *)

This works because Derivative is not a protected function. Of course, just as with the replacement by $\sqrt{x^2}$, this is only valid if you know you're dealing with purely real variables.

To undo the above definition, you can do this:

Derivative[1][Abs][x_] =.

Edit for more generality

If you want to go this route, then the issue might occur that you also want to define the derivative to give an answer at the vertex of the absolute-value function. The correct answer is the Dirac delta function, and to make this come out correctly one could define the general $n$-th derivative as follows:

Derivative[n_][Abs][x_] := 2 Derivative[n - 1][(HeavisideTheta[#] - 1/2)&][x]

The main advantage is that you also get the delta function in the second derivatitve that incorporates the special case where the derivative jumps:

Abs''[1. - a]

(* ==> 2 DiracDelta[1. - a] *)

Answer 3

It seems no one has mentioned ComplexExpand[expr], which "expands expr assuming that all variables are real," as a potential solution; it certainly applies in the example, since a is explicitly assumed to be real.

ComplexExpand will work on the derivative of Abs:

ComplexExpand[Abs'[1 - a]]
(*  1/Sqrt[(1 - a)^2] - a/Sqrt[(1 - a)^2]  *)

but in some cases, it might be more convenient to expand absolute values in the function:

D[ComplexExpand[-Abs[1 - a]], a]
(*  (1 - a)/Sqrt[(1 - a)^2]  *)

Answer 4

As of V11.1 there's RealAbs, whose derivative exists and evaluates automatically:

RealAbs'[1. - x]

(1. - x)/RealAbs[1. - x]