2

I need to find the instantaneous phase and instantaneous frequency for a rotating system. I am having difficulty making the math work with interpolating functions.

First, here is a problem without interpolating functions that I can make work:

phase[t_] := ArcTan[Cos[2*t + .1 t^2], Sin[2*t + .1 t^2]]
Plot[phase[t], {t, 0, 20}]
frequency = D[phase[t], t];
Plot[frequency, {t, 0, 20}, AxesOrigin -> {0, 0}]

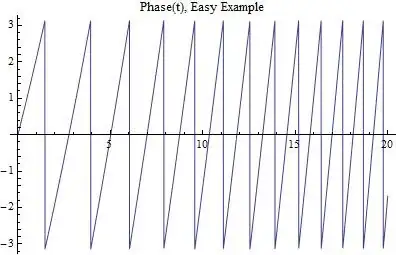
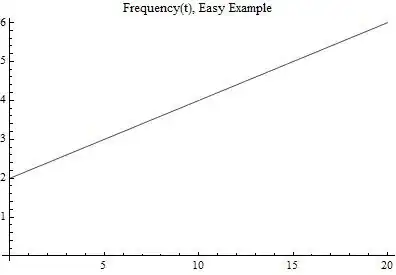
phase vs t freq vs time

In this first example, Mathematica is able to take the derivative of the phase to yield frequency. Now, in 3 dimensions with the Bloch equation:

eqn = {m'[t] == -2*Cross[m[t], {0, 0, 1}], m[0] == {1, 0, 0}}; 
sol1 = NDSolve[eqn, {m}, {t, 0, 20}]  ;
mm[t_] := m[t] /. sol1[[1]];

phase[t_] := ArcTan[First[mm[t]], Last[Most[mm[t]]]];
Plot[phase[t], {t, 0, 20}]
freq[t_] := D[ArcTan[First[mm[t]], Last[Most[mm[t]]]], t];
Plot[freq[t], {t, 0, 20}]

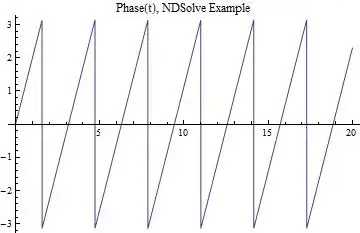
enter image description here

This phase plot looks about the same as the first example. So why can't Mathematica take the derivative? Here is the error Mathematica spits out:

General::ivar: 0.0004085714285714286` is not a valid variable. >>
General::ivar: 0.4085718367346939` is not a valid variable. >>
General::ivar: 0.8167351020408163` is not a valid variable. >>
General::stop: Further output of General::ivar will be suppressed during this calculation. >>

I believe This question might be similar, and this and this both provided a lot of insight, but I've tried every variation I can think of, and can't figure out how to pass this through the derivative.

What to do next? Is it just my getting caught on the notation?

Edit: Original Question About Interpolating Functions Contained Set-Delay Errors; Expanding Question to Focus on Interpolated Function.

With this code, there are no errors. However, there is also no output:

eqn = {m'[t] == -2*Cross[m[t], {0, 0, 1}], m[0] == {1, 0, 0}}; 
sol1 = NDSolve[eqn, {m}, {t, 0, 20}]  ;
mm = m /. sol1[[1]];

phase = ArcTan[First[mm], Last[Most[mm]]]
Plot[phase, {t, 0, 20}]
freq = D[ArcTan[First[mm]], Last[Most[mm]], t];
Plot[freq, {t, 0, 20}]

It is as though nothing happens. The plot thickens when I execute the next code; it shows that Mathematica can perform the the First of the mm and also the derivative of mm. However, with this arrangement it can't perform ArcTan.

eqn = {m'[t] == -2*Cross[m[t], {0, 0, 1}], m[0] == {1, 0, 0}}; 
sol1 = NDSolve[eqn, {m}, {t, 0, 20}]  ;
mm[t_] = m[t] /. sol1[[1]];

Plot[First[mm[t]], {t, 0, 20}] (*This Plot Works*)
dmm = D[mm[t], t];
Plot[First[dmm], {t, 0, 20}](*This Plot Works*)

phase = ArcTan[First[mm[t]], Last[Most[mm[t]]]]

Last::nolast: InterpolatingFunction[{{0.,20.}},{4,3,1,{329},{4},0,0,0,0,Automatic},
{{0.,<<49>>,<<279>>}},{{{1.,0.,0.},{0.,2.,0.}},{{1.,0.000177626,0.},
{-0.000355252,2.,0.}},<<47>>,{{-0.972807,0.231619,0.},{-0.463238,-1.94561,0.}},
<<279>>},{Automatic}][] has a length of zero and no last element. >>

So my troubleshooting tells me that it is possible to take first of an interpolated function, and it is also possible to take the derivative of the interpolated function, but when it encounters them together inside the ArcTan, it isn't able to correctly call the correct direction of the interpolating function vector.

Community
  • 1
Astor Florida
  • 1,326
  • 7
  • 21

2 Answers2

1

A work-around I can think out:

Clear[a, b]
eqn = {m'[t] == -2 Cross[m[t], {0, 0, 1}], m[0] == {1, 0, 0}};
sol1 = NDSolve[eqn, {m}, {t, 0, 20}];

mm = m /. sol1[[1]];
m1 = mm /. {a_, b_, c_} -> a;
m2 = mm /. {a_, b_, c_} -> b;

freq[t_] = D[ArcTan[m1[t], m2[t]], t];

Plot[freq[t], {t, 0, 20}, AxesOrigin -> {0, 0}]

enter image description here

If you have difficulty in understanding, check the InputForm of mm. Also, you may be interested in this and this post.

Community
  • 1
xzczd
  • 65,995
  • 9
  • 163
  • 468
  • This makes a ton of sense - obvious now that I examine it. This was my problem all along. Unfortunately this link doesn't cover substitution rules for vectoral interpolating functions. In retrospect, however, it is obvious. Thank you very much. – Astor Florida Dec 18 '14 at 05:54
1

I'm sure this is a duplicate but my search terms are not on target. The problem has nothing to do with NDSolve.

freq[t_] := D[Exp[t], t];
Plot[freq[t], {t, 0, 20}]

General::ivar: 0.0004085714285714286` is not a valid variable. >>

General::ivar: 0.4085718367346939` is not a valid variable. >>

General::ivar: 0.8167351020408163` is not a valid variable. >>

General::stop: Further output of General::ivar will be suppressed during this calculation. >>

These occur because freq[0.0004085714285714286]` evaluates to

D[Exp[0.0004085714285714286`], 0.0004085714285714286`]

and one cannot take the derivative with respect to 0.0004085714285714286`.

There are various workarounds. Here's another

freq[t0_] := D[Exp[\[FormalT]], \[FormalT]] /. \[FormalT] -> t0;
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Where does the 0.0004085714285714286 come from? Where can I read about this? – Astor Florida Dec 17 '14 at 14:15
  • @axsvl77 It is the first number that Plot plugs into freq[t]. If you search the site, you should be able to find related posts. Ignore the fact that I was unsuccessful at finding them. It's common issue with D, which I've seen several times on the site. – Michael E2 Dec 17 '14 at 14:19
  • @axsvl77 Found it: http://mathematica.stackexchange.com/questions/1301/generalivar-is-not-a-valid-variable-when-plotting-what-actually-causes-this – Michael E2 Dec 17 '14 at 14:23
  • Well, I'm afraid this doesn't solve OP's problem. The true reason is that the mm outputs a list while it is one InterpolatingFunction, so list manipulations like First, Most etc. won't work anymore! – xzczd Dec 17 '14 at 14:47
  • @xzczd I did not notice that part. I would say, however, that the true reason is for the General::ivar messages cited is what I point out. But solving it still leave the problem you point out. – Michael E2 Dec 17 '14 at 17:55
  • This is a great conversation. I will learn from it and change my question. – Astor Florida Dec 17 '14 at 20:44
  • @axsvl77 You might ask another question about how to take the derivative of the parts of a vector-valued interpolation function (without involving Plot in the question). It's interesting and not obvious how to do it. xzczd's could repost the answer and the issue would have a clean Q&A to address. – Michael E2 Dec 17 '14 at 21:16
  • ....Unless it's been asked and answered before, too. – Michael E2 Dec 17 '14 at 21:17
  • @MichaelE2 I have extended my question to be more focused on the primary problem. After a search, I didn't find another question about substitution, and vectoral interpolating functions. Would it be better for me to repost a shorter, more focused question? And delete this one? – Astor Florida Dec 18 '14 at 06:06
  • @axsvl77 I would suggest posting a new one. You might mention and link to this this, but point out the focus on the distinct issue of differentiating parts of vectorial interpolating functions. I would not recommend deleting this one. The community seems to think duplicates help users searching for solutions. For instance, if someone else has a similar problem using NDSolve, they're likely to find this question before the linked duplicate. – Michael E2 Dec 18 '14 at 12:48
  • Ok. I like the interactive process of keeping this website focused and functional. Thanks for keeping everything straight! – Astor Florida Dec 18 '14 at 13:52