How discretize a region placing vertices on a specific non-uniform grid

Question

Given a generic region, for example:

Ω = 
  ImplicitRegion[
   2 x^2 + 3 y^2 + 2 x y - 2 <= 0 ∧ x^2 + y^2 > .1, {x, y}];

and a non-uniform grid, for example:

Ωb = RegionBounds[Ω];
{xg, yg} = 
  N@Map[bound \[Function] 
     Range[bound[[1]], 
      bound[[2]], (bound[[2]] - bound[[1]])/20], Ωb];
{xg, yg} = 
  Map[g \[Function] {g[[1]], 
     Sequence @@ (g[[2 ;; -2]] RandomReal[{1 - .04, 1 + .04}, 
         Length[g] - 2]), g[[-1]]}, {xg, yg}];

which, together, can be shown with:

Ωg = 
  RegionPlot[Ω, AspectRatio -> Automatic];

gg = Graphics[{LightGray,
    Table[
     Line[{{x, Ωb[[2, 1]]}, {x, Ωb[[2, 
         2]]}}], {x, xg}],
    Table[
     Line[{{Ωb[[1, 1]], y}, {Ωb[[1, 2]], 
        y}}], {y, yg}]
    }];

Show[gg, Ωg]

I'm searching a way to discretize the region to a MeshRegion or ElementMesh in such a way that all vertices (MeshCoordinates or incidents) are placed on at least one gridline.

At present I'm working on a routine that discretize the region with BoundaryDiscretizeRegion with a reasonable MaxCellMeasure. Then I'm trying to split all Line mesh cells crossing any gridline into two or more Line such that at least one end is on a gridline. Then I plan to delete vertices not on a grid line and properly reconnect the sourronding vertices.

This is the only way I could think to, but it appear difficult, because there are many branches tho examine.

A more elegant and simple approach would be helpful. For example, there is a way to use ToElementMesh and ToBoundaryMesh to accomplish this task? In the end, the routine should work with thousand of vertices and hundred of gridlines in a reasonable time.

Answer 1

regplt =   RegionPlot[\[CapitalOmega], AspectRatio -> Automatic];

ContourPlot[{2 x^2 + 3 y^2 + 2 x y - 2, x^2 + y^2 - .1}, {x, -1.25, 1.25}, {y, -1.25, 1.25},
Contours -> {{0}}, BaseStyle -> Thick,
GridLines -> {xg, yg}, Method -> {"GridLinesInFront" -> True},
MeshFunctions -> {#1 &, #2 &}, Mesh -> {xg, yg},
MeshStyle -> {Directive[{Red, PointSize[.01]}],
Directive[{Green, PointSize[.01]}]},
ImageSize -> 400, Prolog -> regplt[[1]]]

Update:

... if I have a Region and not its implicit description

you can recover the implicit description of the region using:

Region`RegionProperty[\[CapitalOmega], {x, y},"ImplicitDescription"]

or

Region`RegionProperty[ \[CapitalOmega], {x, y},"FastDescription"][[1, 2]]

to get

-2+2 x^2+2 x y+3 y^2 <= 0 && x^2+y^2 > 0.1 

Answer 2

This is the same idea as unlikely's, which has same following drawback. The discretization of the region makes the boundary piecewise linear and thereby reduces the accuracy. The points found on the grid are points on the linear approximations of the boundary. This causes the boundary to contract further (on the concave side), thereby further reducing the accuracy. Ideally, a root-finding procedure should be applied to adjust the points found in this method toward the boundary of the region. Given that the regions are generic, it seemed difficult to hit on a good generic algorithm. When the equation of the boundary is known, FindRoot is the obvious choice. In other cases, it or something else might be efficient. In any case, I left that adjustment to be done.

The idea is simple. For each boundary line/curve/path, find the grid lines crossed by each segment and solve for the intersections. Do this in order, so that the boundary element of the region can be constructed. The intersections are simple linear equations that can be conveniently solved with Rescale.

snaptogrid[reg_, xg_, yg_] :=
 Module[{ptslists, coords, tpos, 
    xsgn, xgCrossings, xt,   ysgn, ygCrossings, yt},

  ptslists = Function[{component},
     coords = Part[
       MeshCoordinates[component],
       Append[#[[All, 1]], #[[-1, 2]]] &[MeshCells[component, 1] /. Line -> Identity]];
     DeleteDuplicates @
      Flatten[
        Table[
         tpos = t + {0, 1};
         xsgn = Evaluate@UnitStep[-Apply[Times, # - coords[[tpos, 1]]]] &;
         xgCrossings = Extract[xg, SparseArray[xsgn@xg]["NonzeroPositions"]];
         xt = Rescale[xgCrossings, coords[[tpos, 1]], tpos];     (* x grid crossing times *)
         ysgn = Evaluate@UnitStep[-Apply[Times, # - coords[[tpos, 2]]]] &;
         ygCrossings = Extract[yg, SparseArray[ysgn@yg]["NonzeroPositions"]];
         yt = Rescale[ygCrossings, coords[[tpos, 2]], tpos];     (* y grid crossing times *)

         Function[{t}, Rescale[t, tpos, #] & /@ Transpose@coords[[tpos]]] /@ 
          Sort@Flatten[{xt, yt}],                (* convert crossing times to coordinates *)

         {t, Length[coords] - 1}],
       1]
     ] /@ ConnectedMeshComponents[RegionBoundary[reg]];
  BoundaryMeshRegion[
   Flatten[ptslists, 1],
   Sequence @@
    (Line /@ Partition[#, 2, 1, 1] & /@
      (Internal`PartitionRagged[Range@Total[#], #] &[Length /@ ptslists]))
   ]
  ]

OP's example:

bΩ = snaptogrid[BoundaryDiscretizeRegion[Ω], xg, yg]; // AbsoluteTiming
(*  {0.237352, Null} *)

Show[
 bΩ, gg,
 Graphics[{Red, Point[MeshCoordinates[bΩ]]}]
 ]

Note: For alternatives to Internal`ParititionRagged, see Partitioning with varying partition size

Answer 3

MOST RECENT UPDATE

I sligtly revised the code, mainly to avoid NSolve to compute lines intersections and to directly get intersection in the proper order, if possible.

This first helper function, with a binary search algorithm, give the gridline index to wich all coordinates vals given belong, or a half-odd if not on gridline; sameTest allow to configure the accuracy of the check.

BinPositions[vals_, brakes_, sameTest_] :=
 Map[val \[Function] 
   Catch@Module[{lo = 1, mid, hi = Length[brakes], el, res},
     While[lo <= hi, Which[
       TrueQ@sameTest[val, el = brakes[[mid = Floor[(lo + hi)/2]]]], 
       Throw[mid],
       el > val, hi = mid - 1,
       True, lo = mid + 1]];
     lo - 1/2],
  vals]

This second helper function, based on some output of the previous functions, gives the indices of the crossed gridlines. Maybe we can do better.

NearestIntegersBetween = {m, n} \[Function] 
   With[{\[Delta] = n - m, p = IntegerQ[m]}, Which[
     \[Delta] > 1 || \[Delta] == 1 && p, {Ceiling[m], Floor[n]},
     \[Delta] > 0, {Floor[m] + 1},
     \[Delta] == 0 && p, {m, n},
     -\[Delta] > 1 || -\[Delta] == 1 && p, {Floor[m], Ceiling[n]},
     -\[Delta] > 0, {Floor[n] + 1},
     True, {}
     ]];

This third helper function compute the intersections of a line segment with the crossed gridlines, in the order of the segment.

SegmentGridIntersections =
  {x1, y1, x2, y2, xl, yl} \[Function] 
   Module[{m11 = y2 - y1, m12 = x1 - x2, v1 = x1 y2 - x2 y1},
    Which[
     Length@xl == 0,
     {(v1 - m12*yl)/m11, yl}\[Transpose],

     Length@yl == 0,
     {xl, (v1 - m11*xl)/m12}\[Transpose],

     True, Join[
        {(v1 - m12*yl)/m11, 
          yl}\[Transpose], {xl, (v1 - m11*xl)/m12}\[Transpose]
        ] // Sort // If[x1 <= x2, #, Reverse@#] &
     ]
    ];

This last helper function process a single contour of a MeshRegion:

AdjustPolygonToGrid[vertices_, grids_, sameTest_] :=
  Module[{positions, lines},
   positions = MapThread[BinPositions[#1, #2, SameTest -> sameTest] &, {vertices\[Transpose], grids}]\[Transpose];
   lines = Apply[NearestIntegersBetween,Transpose[Partition[positions, 2, 1], {1, 3, 2}], {2}];
   lines = MapThread[Extract, {grids, Map[List, lines\[Transpose], {2}]}]\[Transpose];
   MapThread[SegmentGridIntersections[Sequence @@ Flatten@#1, Sequence @@ #2] &, {Partition[vertices, 2, 1], lines}] // Flatten[#, 1] & // Append[#, #[[1]]] &
   ];

This main function finally process a whole MeshRegion.

AdjustMeshToGrid[meshRegion_, grids_, sameTest_] :=
 Module[{polygons, vertices, map},
  polygons = meshRegion["BoundaryPolygons"][[All, 1]];
  polygons = AdjustPolygonToGrid[#, grids, sameTest] & /@ polygons;

  vertices = DeleteDuplicates[Join @@ polygons];
  map = AssociationThread[vertices, Range@Length@vertices];

  (* Restituisce la mesh adattata *)
  BoundaryMeshRegion[vertices, 
   Sequence @@ Line /@ Map[map, polygons, {2}]]
  ]

With thid code there are the results compared to the routine proposed by @Michael E2 on a uniform grid.

timeAvg = 
  Function[func, 
   Do[If[# > 0.3, Return[#/5^i]] & @@ Timing@Do[func, {5^i}], {i, 0, 
     15}], HoldFirst];

\[CapitalOmega] = 
  ImplicitRegion[
   2 x^2 + 3 y^2 + 2 x y - 2 <= 0 \[And] x^2 + y^2 > .1, {x, y}];
\[CapitalOmega]b = RegionBounds[\[CapitalOmega]];

data = Table[Module[{grids, mesh, n},
    grids = 
     N@Map[range \[Function] 
        Range @@ 
         Append[range, -Subtract @@ range/20/2^k], \[CapitalOmega]b];
    (*grids=Union/@Map[g\[Function]{g[[1]],
    Sequence@@(g[[2;;-2]]RandomReal[{1-.02,1+.02},Length[g]-2]),
    g[[-1]]},grids];*)
    n = Length@First@grids;
    mesh = 
     BoundaryDiscretizeRegion[\[CapitalOmega], 
      MaxCellMeasure -> Mean@Flatten[Differences /@ grids]];
    <|
     "Gridlines Count" -> n,
     "AdjustMeshToGrid" -> (AdjustMeshToGrid[mesh, grids, 
         Abs[#1 - #2] <= 10.^-10 &] // timeAvg),
     "snaptogrid" -> (snaptogrid[mesh, Sequence @@ grids] // timeAvg)
     |>
    ], {k, 0, 10}] // Dataset

ListPlot[
 Values@*Normal /@ {data[
    All, {"Gridlines Count", "AdjustMeshToGrid"}], 
   data[All, {"Gridlines Count", "snaptogrid"}]},
 Joined -> True, PlotLegends -> {"AdjustMeshToGrid", "snaptogrid"}, 
 Frame -> True, Mesh -> Full, GridLines -> Automatic, 
 FrameTicks -> Automatic, PlotRange -> All]

FIRST ANSWER

I finally found a relatively short way to do. Not perfect, many special cases should be handled. Michael E2 routine permorms better on small uniform grids. I don't know why but on small random grids the rating is reversed.

I can do:

mesh = BoundaryDiscretizeRegion[\[CapitalOmega]];
polygons = mesh["BoundaryPolygons"][[All, 1]];
polygons = 
  AdjustPolygonToGrid[#, {xg, yg}, Abs[#1 - #2] <= 10^-6 &] & /@ 
   polygons;
vertices = DeleteDuplicates[Join @@ polygons];
verticesMap = AssociationThread[vertices, Range@Length@vertices];
adjustedMesh = BoundaryMeshRegion[vertices, 
 Sequence @@ Line /@ Map[verticesMap, polygons, {2}]];

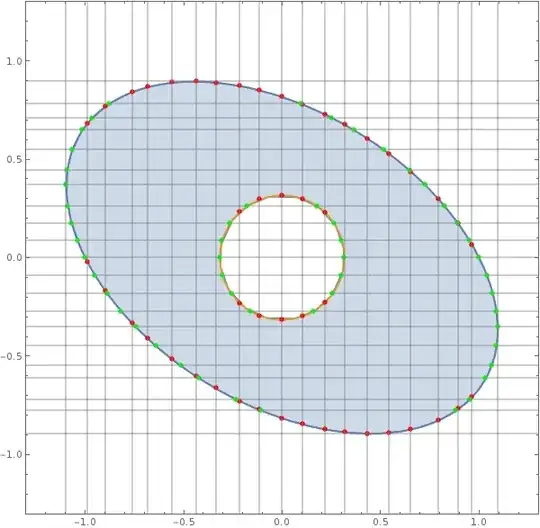
Graphics[{Opacity[.7], HighlightMesh[adjustedMesh, 0]["Show"][[1]]}, 
 Frame -> True, GridLines -> {xg, yg}, 
 GridLinesStyle -> Darker[LightGray]]

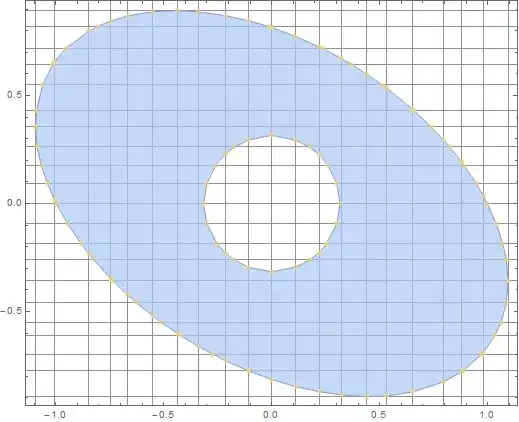
with the main helper's function:

AdjustPolygonToGrid[vertices_, grids_, sameTest_] :=
 Module[{positions, v1, p1},
  positions = 
   MapThread[
     BinPositions[#1, #2, 
       SameTest -> sameTest] &, {vertices\[Transpose], 
      grids}]\[Transpose];
  {v1, p1} = {vertices[[1]], positions[[1]]};
  Apply[{v2, p2} \[Function] Module[{lines, vlnew},
         If[AnyTrue[p2, IntegerQ], Sow[v2],
          lines = MapThread[NearestIntegersBetween, {p1, p2}];
          If[lines =!= {{}, {}},
           lines = MapThread[#1[[#2]] &, {grids, lines}];

           lines = 
            RegionUnion @@ 
             Flatten@{InfiniteLine[{#, 0}, {0, 1}] & /@ lines[[1]], 
               InfiniteLine[{0, #}, {1, 0}] & /@ lines[[2]]};

           vlnew = 
            Block[{x, y}, {x, y} /. 
              NSolve[{x, y} \[Element] 
                 Line[{v1, v2}] \[And] {x, y} \[Element] lines, {x, 
                y}, Reals]];

           vlnew = 
            If[OrderedQ[{v1, v2}], Sort[vlnew], Reverse@Sort[vlnew]];
           Sow /@ vlnew;
           ];
          ];
         {v1, p1} = {v2, p2}
         ], RotateLeft@Transpose@{vertices, positions}, {1}] //
      Reap // Last // Last // Append[#, #[[1]]] &
  ]

and two simple helper's function:

BinPositions[vals_, brakes_, sameTest_] :=
 Map[val \[Function] 
   Catch@Module[{lo = 1, mid, hi = Length[brakes], el, res},
     While[lo <= hi, Which[
       TrueQ@sameTest[val, el = brakes[[mid = Floor[(lo + hi)/2]]]], 
       Throw[mid],
       el > val, hi = mid - 1,
       True, lo = mid + 1]];
     lo - 1/2],
  vals]

NearestIntegersBetween = {m, n} \[Function] 
   Which[#1 < #2, {##}, #1 == #2, {#1}, 
      True, {}] & @@ ({Floor[#1] + 1, Ceiling[#2 - 1]} & @@ 
      Sort[{m, n}]);

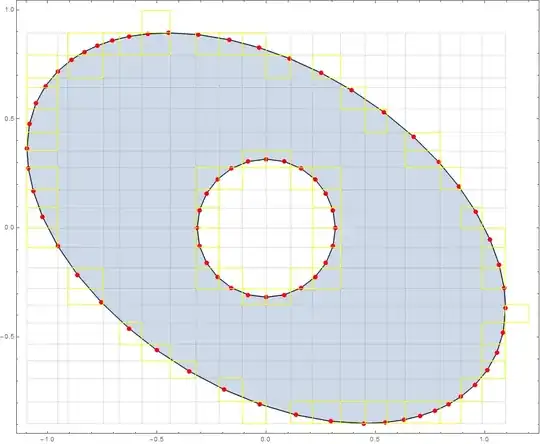
For example original and ajusted small polygon:

polygon = mesh["BoundaryPolygons"][[1, 1]];
AdjustPolygonToGrid[polygon, {xg, yg}, Abs[#1 - #2] < 10^-6 &];
Graphics[{
  Opacity[.5], LightGray, Polygon@polygon, Opacity[1],
  Orange, AbsolutePointSize[Large], Point@polygon,
  Blue, Line@%,
  Red, AbsolutePointSize[Medium], Point@%,
  Green, Point@polygon[[1]],
  Yellow, Point@polygon[[2]]},
 PlotRange -> RegionBounds@Line@polygon, 
 PlotRangePadding -> Scaled[.05], Frame -> True, 
 GridLines -> {xg, yg}, GridLinesStyle -> Darker[LightGray]]

The overall procedure is a bit slow, also with this simple mesh. Some special cases are not handled (for example if two or more vertices of the original mesh are on the same cell edge).

Answer 4

Building on the trick of kguler and on the @user21 recommendations I ends up with the following approach.

For many reason my actual interest is on first-order meshes and on a MeshRegion-type output. However, I used the some services of FEM toolbox and particularly of NumericalRegion.

• Its "BoundaryFunction" property with FindRoot is useful to "improve" RegionPlot output. I don't know if we can easily build this compiled function directly from a generic Region.

• For some misterious (for me) reason, the output of RegionPlot[numericalRegion["Predicates"], ...] appears more accurate than RegionPlot[symbolicRegion, ...]. This turns out to be very important to get a valid MeshRegion with the actual implementation because...

In the RegionPlot output improvement phase boundary vertices are moved, and a boundary vertex can cross a mesh line. So, at some times we need to reorder the vertices on a boundary, otherwise we can get an invalid / self-crossing boundary. This becomes a problem for fine meshes (in the following samples for Mesh option >= 50. A more accurate RegionPlot output is helpful to reduce the need of reordering.

I'd appreciate any suggestion to detect and fix this problem and to improve the whole implementation.

<< NDSolve`FEM`

Options[ConstrainedRegionPlotMeshGenerator] = {Mesh -> Automatic, PlotPoints -> Automatic, MaxRecursion -> Automatic};
ConstrainedRegionPlotMeshGenerator[region_NumericalRegion, opts : OptionsPattern[]] := 
 ConstrainedRegionPlotMeshGeneratorCore[region, opts] // ToBoundaryMesh
ConstrainedRegionPlotMeshGenerator[region_ /; ConstantRegionQ[region],
   opts : OptionsPattern[]] := 
 ConstrainedRegionPlotMeshGeneratorCore[ToNumericalRegion@region, opts]

ConstrainedRegionPlotMeshGeneratorCore[region_NumericalRegion, 
   opts : OptionsPattern[]] :=
  Module[{g, mptsx, mptsy, mpts, blns, mptq, grids, xg, yg, \[Delta], 
    pts, ptsx, ptsy, x, y},

   (* draw region with RegionPlot and extract the GraphicsComplex *)
   g = First@RegionPlot[
      (*region["SymbolicRegion"],*)
      region["Predicates"],
      Evaluate[
       Sequence @@ 
        MapThread[
         Prepend, {region["Bounds"], region["PredicateVariables"]}]],
      Frame -> False, PlotStyle -> None, BoundaryStyle -> Red, 
      MeshStyle -> Blue,
      Evaluate@FilterRules[{opts}, {Mesh, PlotPoints, MaxRecursion}]];

   (* get mesh lines endpoints and boundary lines *) 
   {mptsx, mptsy} = 
    Union @@@ 
     Cases[g, {Blue, lines___Line} :> {lines}, \[Infinity]][[All, All,
        1, {1, -1}]];
   If[Intersection[mptsx, mptsy] =!= {}, Return[$Failed]]; (* 
   Unsupported at present *)
   mpts = DeleteDuplicates@Join[mptsx, mptsy];
   blns = 
    Cases[g, {Directive[___, Red, ___], lines___Line} :> 
      lines, \[Infinity]];

   (* build closed boundary lines selecting boundary lines vertices \
that are also on mesh lines *)
   mptq = AssociationThread[mpts, Range@Length@mpts];
   blns = Map[DeleteMissing[mptq /@ #] &, blns, {2}];
   blns = 
    Map[If[Last@# == First@#, #, Append[#, First@#]] &, blns, {2}];

   (* improve  boundary vertices position *)
   \[Delta] = region["BoundaryFunction"];
   ptsx = {#[[1]], 
       y /. FindRoot[\[Delta][{#[[1]], y}], {y, #[[2]]}]} & /@ 
     g[[1, mptsx]];
   ptsy = {x /. 
        FindRoot[\[Delta][{x, #[[2]]}], {x, #[[1]]}], #[[2]]} & /@ 
     g[[1, mptsy]];
   pts = Join[ptsx, ptsy];

   (* build result*)
   BoundaryMeshRegion[pts, Sequence @@ blns]
   ];

For example, with a uniform mesh, and a MeshRegion output:

ConstrainedRegionPlotMeshGenerator[\[CapitalOmega], Mesh -> {5, 10}]

With an explicit, non-uniform grid, and a MeshRegion output:

Show[
 ConstrainedRegionPlotMeshGenerator[\[CapitalOmega], Mesh -> grids],
 GridLines -> grids, GridLinesStyle -> LightGray, 
 Method -> {"GridLinesInFront" -> True}
 ]

With an explicit, non-uniform grid, and an ElementMesh output:

mesh = ToBoundaryMesh[\[CapitalOmega], 
  "BoundaryMeshGenerator" -> {ConstrainedRegionPlotMeshGenerator, 
    Mesh -> grids}]

Show[
 mesh["Wireframe"],
 mesh["Wireframe"["MeshElement" -> "PointElements"]],
 GridLines -> grids, GridLinesStyle -> LightGray
 ]