4

desired histogram

I wanted to draw a histogram as in the photo above, I typed the command:

Histogram[{{11.945, 11.96, 11.975, 11.99, 12.005, 12.02, 12.035}, {3, 9, 13, 21, 9, 4, 1}}]

I got completely wrong chart. What should I do to correct that ?

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
Perw
  • 41
  • 1
  • 1
  • 2

5 Answers5

7

Specifically, this is what @Yves recommendation looks like.

BarChart[{{3, 9, 13, 21, 9, 4, 1}}, 
ChartLabels -> {"11.945", "11.96", "11.975", "11.99", "12.005", "12.02", "12.035"}]

bar chart

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • The presence of a smooth histogram in the OP's graphic suggests that the original data is continuous, a bar chart may not be as appropriate as a histogram. – A.G. Jan 03 '15 at 21:00
4

Adding the curve to @bbgodfrey's answer

values = {11.945, 11.96, 11.975, 11.99, 12.005, 12.02, 12.035};

freq = {3, 9, 13, 21, 9, 4, 1};

Manipulate[
 f = ListInterpolation[freq,
   InterpolationOrder -> io];
 Show[
  BarChart[{freq}, ChartLabels -> values], Plot[f[x], {x, 1, Length[freq]},
   PlotStyle -> Darker[Red, .3]]],
 {{io, 2, "Interpolation\nOrder"}, Range[Length[freq] - 1]}]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
4

When dealing with this type of data, use the WeightedData construct (please look it up).

data = WeightedData[{11.945, 11.96, 11.975, 11.99, 12.005, 12.02, 12.035}, {3, 9, 13, 21, 9, 4, 1}]

Histogram[data]

Histogram[data, 6]

Mathematica graphics

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • @Kuba I don't understand what you mean. Are you referring to the recently asked question? There "data" is a number. He is working with dates (i.e. numbers). A "histogram" only makes sense for numbers because it involves binning, i.e. comparing if the data is larger than a bin's lower bound and smaller than its upper bound. Otherwise we call it counts, not a histogram: Counts[{"a","a","b"}]. – Szabolcs Apr 19 '17 at 14:32
  • Yep, I agree about what that means. I just wrongly ignored that based on vote counts suggesting something different. Sorry for confusion. – Kuba Apr 19 '17 at 14:52
1

To use Histogram with this type of data, Szabolcs's approach is the most direct and convenient. An alternative approach is to use bin and height specifications obtained from the table directly in Histogram. Taking the first column as the centers of equally spaced bins, we construct bins by shifting the centers. We use artificial data (say, {0}) as the first argument of Histogram, and use frequencies directly in the third argument. Finally, we add the line obtained from bin centers and frequencies as Epilog.

bincenters = {11.945, 11.96, 11.975, 11.99, 12.005, 12.02, 12.035};
spacing = First @ Differences @ bincenters;
bins = {Append[bincenters - spacing/2, Last[bincenters] + spacing/2]};
frequencies = {3, 9, 13, 21, 9, 4, 1};

Panel @ Histogram[{0}, bins, frequencies &, ChartStyle -> 60,
  PlotRange -> {0, 25}, AspectRatio -> 1, Ticks -> {bincenters, Automatic},
  Epilog -> (ListLinePlot[Transpose[{bincenters, frequencies}],
      PlotStyle -> Thick, InterpolationOrder -> 2][[1]])]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
1

The fact that your histogram comes with a smooth histogram curve suggests that it comes from continuous data : observations are not all equal to 11.945, 11.96, etc. For that reason, using BarChart is not appropriate, at least from a statistical point of view.

In order to use Histogram you first need to generate the raw data from the values and frequencies you have. Taking the values that are in your frequency table you can do

val = {11.945, 11.96, 11.975, 11.99, 12.005, 12.02, 12.035};
freq = {3, 9, 13, 21, 9, 4, 1};
n = Length[val];
w = 0.015; (* bin width *)
data = Flatten@Array[Table[val[[#]], {freq[[#]]}] &, n]

with output

{11.945, 11.945, 11.945, 11.96, 11.96, 11.96, 11.96, 11.96, 11.96, \
11.96, 11.96, 11.96, 11.975, 11.975, 11.975, 11.975, 11.975, 11.975, \
11.975, 11.975, 11.975, 11.975, 11.975, 11.975, 11.975, 11.99, 11.99, \
11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, \
11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, 11.99, \
12.005, 12.005, 12.005, 12.005, 12.005, 12.005, 12.005, 12.005, \
12.005, 12.02, 12.02, 12.02, 12.02, 12.035}

and now

Histogram[data, {w}, ColorFunction -> "Rainbow"]

Mathematica graphics

The problem however is that the SmoothHistogram[data] will not output what you expect:

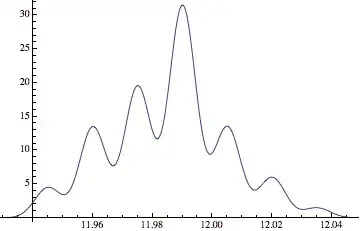
Mathematica graphics

the reason being that the data used to create the smooth histogram in your photo is likely not the one given in the frequency table. More likely, the values are more or less uniformly distributed in each bin as opposed to being all equal to bin centers.

There is no way to recover neither the exact data nor its unique smooth histogram from grouped data. At best you could the fake some data using a uniform distribution in each bin:

data = Flatten@
   Array[RandomVariate[
      UniformDistribution[{val[[#]] - w/2, val[[#]] + w/2}], 
      freq[[#]]] &, n];

Show[Histogram[data, {val[[1]] - w/2, val[[n]] + w/2, w},ColorFunction -> "Rainbow"],
 SmoothHistogram[data]]

Mathematica graphics

(of course the smooth histogram, coming from randomly generated data, will change at each evaluation).

A.G.
  • 4,362
  • 13
  • 18
  • could you explain what exactly do this formula

    Flatten@Array[Table[val[[#]], {freq[[#]]}] &, n]

    because I'm a beginner and it is my first time when I see that kind of stuff, I found what do Flatten and Array in help windows but I can not found what do those Flatten@Array and what means #

     – Perw Feb 07 '15 at 15:29
  • @Perw @ is an alternative form for applying a function: f@x is the same as f[x]. # and & are yet another way of defining a function, # is the variable and & ends the function definition. You will find all that in books and online resources on Mathematica programming. – A.G. Feb 09 '15 at 15:39