11

I need a function for a series of joined slopes and my solution feels a bit kludgy. Is there a better way?

A list of pairs of transition points and slopes:

dat = {{0, 0}, {18, 1}, {70, 1/4}, {90, -1}, {110, 2}};

Build a function:

ClearAll[f]
f[0] = 0;
Cases[
  Partition[dat, 2, 1],
  {{lo_, _}, {hi_, slope_}} :>
    (f[x_ /; x <= hi] := f[lo] + slope (x - lo))
];

Plot it:

Plot[f[x], {x, 0, 110}, AspectRatio -> Automatic, GridLines -> {{18, 70, 90}, None}]

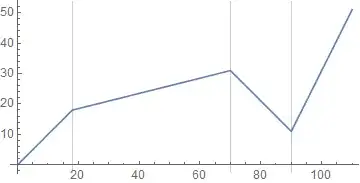
enter image description here

The input format (dat) is arbitrary and could possibly be better too.

Performance

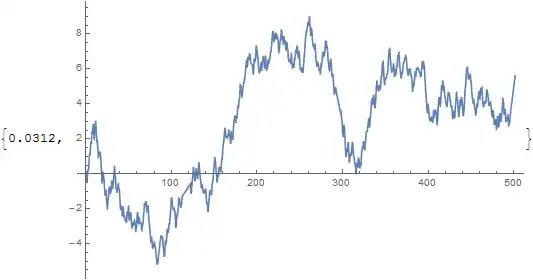
There are presently three answers using Interpolation including my own. Speed of evaluation of the InterpolatingFunction appears to be the same in each case. Here is a comparison of the speed of generation in 10.1.0 under Windows. I shall cheat for my method by using a pure function (g2) which trades clarity for speed. (Spoiler: it still doesn't win.)

SeedRandom[1]
dat = {Accumulate @ RandomReal[{0, 1}, 1000], RandomReal[{-1, 1}, 1000]}\[Transpose];

RepeatedTiming[
  f1[x_] = Integrate[Interpolation[dat, InterpolationOrder -> 0][x], x];
]

{0.00215, Null}

g2 = {#2[[1]], #[[2]] + (#2[[1]] - #[[1]]) #2[[2]]} &;

RepeatedTiming[
  f2 = Interpolation[FoldList[g2, dat], InterpolationOrder -> 1];
]

{0.00145, Null}

RepeatedTiming[
  x = dat[[;; , 1]];
  y = {#}~Join~(# + Accumulate[Differences[x] dat[[2 ;;, 2]]]) &@dat[[1, 2]];
  f3 = Interpolation[Transpose[{x, y}], InterpolationOrder -> 1];
]

{0.000972, Null}

So it seems Algohi's code is fastest at less than half the time of Integrate.
(His answer deserves more votes!)

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • @David Sorry for being vague. I'm tired and can't think clearly. :-p I did not mean slope in the proper sense, just the common one. The function behaves just as I want despite the poor terminology. In the dat format the pairs {v, s} should be read as "use slope s up to value v" -- the {0, 0} what just added to make my kludgy function work. – Mr.Wizard Jan 09 '15 at 22:14
  • What would you want for your graph if your data did not form a continuous function, e.g., {{0,0}, {10,1}, {20, 5}, {30, -8}}? – David G. Stork Jan 09 '15 at 22:17
  • @DavidG.Stork: The graph will always be continuous on $(-\infty,m]$ where $m$ is the max bound, irregardless of what data is used. Try using your example with his plot method. – DumpsterDoofus Jan 09 '15 at 22:19
  • OK. Fair enough. But here's how I would clarify and improve the question: "Given a sequential list of pairs {y_i, slope_i}, create and plot the continuous, piecewise linear function of x that goes from point {x_i, y_i} through {x_(i+1), y_(i+1)} with slope slope_(i+1). (Note that you're effectively solving for the x_i; note too the slope of the first pair in the list is never used.)" – David G. Stork Jan 09 '15 at 23:04
  • I would also not use the phrase "joined slopes" in the title, since a slope is a real-valued number and is never "joined." I'd suggest a title such as this: "Create a piecewise linear function from a list of ordinates and scalar slopes." Or something like that. – David G. Stork Jan 09 '15 at 23:27
  • The current problem statement refers to "transition points," but in a two-dimensional plot one generally understands a "point" to be specified by a two-dimensional coordinate; instead, the current problem means a single ordinate value. Very awkward. – David G. Stork Jan 09 '15 at 23:42
  • @David As stated I was tired when I wrote this question and I know it could have been written better. Please, would you consider editing it yourself with the improvements you suggest? One exception however: the input format is not important, only the result, so for example the slope in the first pair or the entire first pair could be omitted if desired so long as the solution works with that. – Mr.Wizard Jan 10 '15 at 07:03
  • 1
    "vertically offset slightly" - you know different functions that have the same derivative differ only by an arbitrary constant, yes? :) – J. M.'s missing motivation May 25 '15 at 11:21
  • @J. M. Now that you ask it like that I suppose so. :-) Is there a simple way to adjust that constant in the case of the Accepted answer, inside the interpolating function? I mean not defining f[x_] := ... + 0.1. Just curious. – Mr.Wizard May 25 '15 at 11:32
  • 1
    For the case of the accepted answer, I think turning the indefinite integral into a definite one (thus, enforcing a boundary condition) should work; if memory serves, the indefinite integration happens to pick the particular integral that is zero at the left endpoint. – J. M.'s missing motivation May 25 '15 at 11:39

5 Answers5

23

Integrate the zero-order interpolation of the data:

f[x_] = Integrate[Interpolation[dat, InterpolationOrder -> 0][x], x];
Plot[f[x], {x, 0, 110}, AspectRatio -> Automatic, GridLines -> {{18, 70, 90}, None}]

enter image description here

It can efficiently plot piecewise functions with thousands of transition points in milliseconds:

dat = {Accumulate@RandomReal[{0, 1}, 1000], RandomReal[{-1, 1}, 1000]}\[Transpose];
f[x_] = Integrate[Interpolation[dat, InterpolationOrder -> 0][x], x];
Timing@Plot[f[x], {x, dat[[1, 1]], dat[[-1, 1]]}]

enter image description here

DumpsterDoofus
  • 11,857
  • 1
  • 29
  • 49
  • See, I had a feeling I was missing something like this. Thanks. :-) – Mr.Wizard Jan 10 '15 at 07:06
  • Following my usual practice I shall wait 24 hours from posting the question before Accepting an answer, but I don't imagine this will be beaten. – Mr.Wizard Jan 10 '15 at 07:35
  • 1
    @Mr.Wizard The cool thing about Integrate here is that it incorporates the derivative info from Interpolation[dat,..] into the integral. It doesn't make a difference here, but it does when integrating a continuous interpolating function. And it has only half the speed of the Accumulate[Differences[dat[[All, 1]]] dat[[2 ;;, 2]]] method. I found the FoldList method slow on DumpsterDoofus's bigger example, but it seems to be closer this morning. I was tired last night and failed to post an answer. – Michael E2 Jan 10 '15 at 16:57
  • 1
    To clarify: The output of Integrate is an InterpolatingFunction that has derivative information stored in it; namely, the values of the derivative at the transition points are specified to be the values the input function. Examine the "dataDerivative" and "basicInterpolatingUnit" fields as defined in this answer, which can be extracted with Extract[Head[f2[x]], {{2, 3}, {4}}]. (Note the third element, the input grid, is missing from the answer.) -- Sorry, I felt I was a little vague, so now I'm over-specific. ;) – Michael E2 Jan 10 '15 at 20:39
  • A variation of this one might try is to form a piecewise-constant function from the given derivatives and then use DSolve[] (if using Piecewise[] or UnitStep[]) or NDSolve[] (if using Interpolation[]) to integrate this piecewise constant function. – J. M.'s missing motivation May 25 '15 at 11:23
  • @J. M. I hope soon that you are able to implement that yourself. – Mr.Wizard May 25 '15 at 11:34
10

This is a typical Finite Difference Method.

x = dat[[;; , 1]];
y={#}~Join~(# + Accumulate[Differences[x] dat[[2 ;;, 2]]]) &@dat[[1, 2]];

Now

f = Interpolation[Transpose[{x, y}], InterpolationOrder -> 1];
Plot[f[x], {x, 0, 110}, AspectRatio -> Automatic,GridLines -> {x, None}]

enter image description here

Basheer Algohi
  • 19,917
  • 1
  • 31
  • 78
6

funny I just worked this up for this answer here : https://mathematica.stackexchange.com/a/71427/2079

 dat = {{0, 0}, {18, 1}, {70, 1/4}, {90, -1}, {110, 2}};
 xmap[x_] = 
    Piecewise[
       Fold[Append[#, {(#[[-1, 1]] /. 
         x -> (Last@Last@Last@#)) + #2[[2]] (x - (Last@Last@Last@#)),
         x < #2[[1]]}] &, {{x dat[[2, 2]], x < dat[[2, 1]]}}, dat[[3 ;;]]]];
 Plot[xmap[x], {x, 0, 110}]

enter image description here

Community
  • 1
george2079
  • 38,913
  • 1
  • 43
  • 110
  • Thanks for the implementation. I considered using Piecewise but it seemed even more convoluted, and from this it looks like it is. Nevertheless +1. – Mr.Wizard Jan 10 '15 at 07:10
5

Although I like DumpsterDoofus's answer a lot more, now that I am properly awake I realize this works:

dat = {{0, 0}, {18, 1}, {70, 1/4}, {90, -1}, {110, 2}};

g[{x_, y_}, {X_, Y_}] := {X, y + (X - x) Y}

f2 = Interpolation[FoldList[g, dat], InterpolationOrder -> 1];

Plot[f2[x], {x, 0, 110}, AspectRatio -> Automatic, GridLines -> {{18, 70, 90}, None}]

enter image description here

Embarrassing that I found that so difficult yesterday but such is life. :^)

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • I was going to post fun[p_, q_] := p + (q[[1]] - p[[1]]) {1, q[[2]]} llp[d_] := ListLinePlot[FoldList[fun[#1, #2] &, d]] . However, as this is essentially that same approach I will not but i find it reassuring...DumpsterDoofus answer is wonderful and I have voted for it.... – ubpdqn May 25 '15 at 03:20
3

Here is the method I was alluding to in a comment to DumpsterDoofus's answer:

dat = {{0, 0}, {18, 1}, {70, 1/4}, {90, -1}, {110, 2}};

(* DumpsterDoofus's solution *)
fd[x_] = Integrate[Interpolation[dat, InterpolationOrder -> 0][x], x];

{xa, ya} = Transpose[dat];

f1 = y /. First[DSolve[{y'[x] == First[ya] + Differences[ya].UnitStep[x - Most[xa]],
                       y[0] == 0}, y, x]];
f2 = y /. First[DSolve[{y'[x] ==
                Piecewise[Transpose[{Rest[ya], #1 <= x < #2 & @@@ Partition[xa, 2, 1]}], 0],
                y[0] == 0}, y, x]];

The three are identical within the domain implied by dat:

Plot[{fd[x], f1[x], f2[x]}, {x, 0, 110}, AspectRatio -> Automatic, 
     GridLines -> {{18, 70, 90}, None}]

three piecewise linear functions

but f1 and f2 differ in their extrapolation behavior to the right:

Plot[{f1[x], f2[x]}, {x, 90, 120}, PlotRange -> All]

extrapolated piecewise linear functions

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574