6

A certain research paper gives a recipe for building Amman-Beenker tilings as a special type of cut-and-project algorithm. The result is usually a pleasant kind of aperiodic tiling shape.

The algorithm defines two sets of vectors $a_k$ and $a_k^\ast$ which are in a sense dual to one another. Using the first set of vectors we look for integer combinations of the vectors lying in a unit octagon:

$$ U = \{ (u_1, u_2, u_3, u_4) \in \mathbb{Z}^4 : \mathrm{Re} \big[e^{2\pi i m/8}\sum a_k^\ast u_k \big] < 1\}$$

Then we take those same vectors and transcribe them from cut-space to project-space using the $\ast$-map.

$$ V = \{ \vec{a}\cdot \vec{u} : \vec{u} \in U \}$$

This is very similar to what one would find in de Brujin's paper

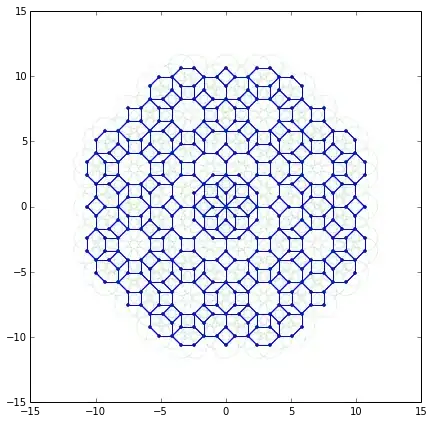
Using brute force, I computed the vertices and found that certain vertices are missing. Could it be that the octagon criterion is wrong? What is the correct size of the octagon?

A general idea could suffice but if you get a working code, I would love to see yours

From What is Aperiodic Order? - Baake Grimm Moody

enter image description here

My result: notice the missing vertices.

enter image description here

The question how to generate no-periodic tilings asks about a different cut and project tiling and uses a substitution method. There are other good tiling questions on this page as well.

Community
  • 1
john mangual
  • 163
  • 4
  • 1
    Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Read the faq! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! – Michael E2 Jan 18 '15 at 01:35

1 Answers1

3

I also stumbled here. But very careful reading of the article reveals that the octagon has unit edge length, thus instead of Re[...]<1, the correct expression is Re[...]<1/2/Tan[Pi/8] (=~1.20711). And then the method works and there are no missing vertices.

lazadugi
  • 31
  • 2