I need to generate nonperiodic tilings which are similar to the attached figure (kite-domino tiling). I was thinking the code is similar to the code for the Penrose tiling. However, that code is too complicated for me to digest at this time.
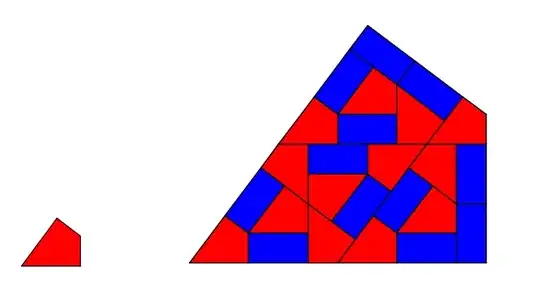
I need to generate nonperiodic tilings which are similar to the attached figure (kite-domino tiling). I was thinking the code is similar to the code for the Penrose tiling. However, that code is too complicated for me to digest at this time.

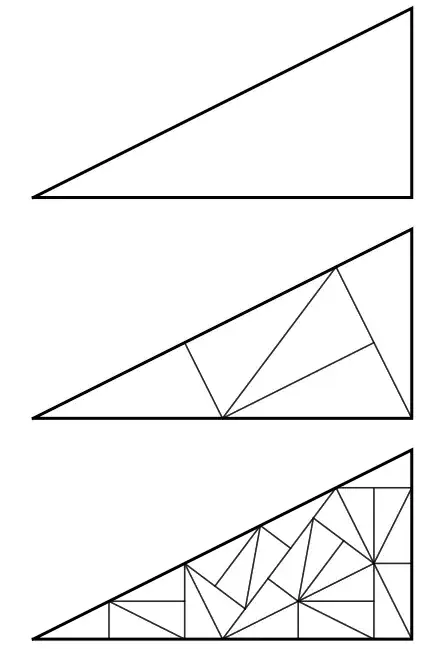
The kite-domino tiling is based the pinwheel tiling which is falls out of a particular decomposition of a right triangle with legs of length 1 and 2. In the code that follows, rt[{a,b,c}] represents such a right triangle and dissect indicates how such a triangle should be decomposed into smaller copies of itself. We simply iterate the dissect function on an initial configuration.
dissect[rt[{a_, b_, c_}]] := Module[
{d, e, f, g},
d = c + ((a - c).(b - c))/((a - c).(a - c)) (a - c) // N;
e = (a + b)/2 // N;
f = b + ((d - b).(e - b))/((d - b).(d - b)) (d - b) // N;
g = a + ((e - a).(c - a))/((c - a).(c - a)) (c - a) // N;
{rt[{a, g, e}], rt[{d, g, e}],
rt[{e, f, d}], rt[{e, f, b}],
rt[{b, d, c}]}];
dissect[l_List] := dissect /@ l;
init = {rt[{{0, 0}, {2, 0}, {2, 1}}]};
iterated = NestList[dissect, init, 2];
GraphicsColumn[Graphics[{
{Thick, Line[{{0, 0}, {2, 0}, {2, 1}, {0, 0}}]},
# /. rt[{a_, b_, c_}] ->
{Opacity[0.6], Line[{a, b, c, a}]}}] & /@ iterated]
Now, if we merely delete each hypotenuse, we already obtain something close to what you want. We can also expand the initial configuration to include a whole rectangle.
init = {rt[{{0, 0}, {2, 0}, {2, 1}}], rt[{{2, 1}, {0, 1}, {0, 0}}]};
Graphics[Nest[dissect, init, 4] /. rt[{a_, b_, c_}] -> Line[{a, b, c}]]

It's trickier to distinguish the kites from the dominoes. I'm certain there's a better way to do this, but one approach is to merge the triangles we've just generated. This is not so simple because, often, the a1 in rt[{a1,b,c1}] and the a2 in rt[{a2,d,c1}] may be very close but not equal. The following attempts to deal with that
Needs["HierarchicalClustering`"]
canonicalFunction[nonCanonicalValues_List] := Module[
{heirarchy, MyClusters, segregate, cf, clusters,
canonicalValues},
Quiet[heirarchy = Agglomerate[N[nonCanonicalValues],
DistanceFunction -> EuclideanDistance,
Linkage -> "Average"]];
segregate[Cluster[cl1_, cl2_, d_, _, _], tol_] :=
MyClusters[cl1, cl2] /; d > tol;
segregate[mine_MyClusters, tol_] :=
segregate[#, tol] & /@ mine;
segregate[x_, _] := x;
cf[cl_Cluster] := ClusterFlatten[cl];
cf[x_] := {x};
clusters = cf /@
List @@ Flatten[FixedPoint[segregate[#, 10^(-12)] &,
MyClusters[heirarchy]]];
canonicalValues = Chop[First /@ clusters];
toCanonical[x_] := First[Nearest[canonicalValues][x]];
toCanonical];
pts = Partition[Flatten[iterated /. rt -> Sequence], 2];
cf = canonicalFunction[pts];
gathered =
GatherBy[Flatten[iterated], Sort[cf /@ {#[[1, 1]], #[[1, 3]]}] &];
preserved = Select[gathered, #[[1, 1, 1]] == #[[2, 1, 1]] &];
flipped = Select[gathered, #[[1, 1, 1]] == #[[2, 1, 3]] &];
join[{rt[{a_, b_, c_}], rt[{_, d_, _}]}] := Polygon[{a, b, c, d}];
Graphics[{EdgeForm[Black],
{Darker[Red], join /@ flipped},
{Gray, join /@ preserved}
}]

rt1s end up forming some of the dominoes and the rt2s end up forming the kites and the rest of the dominoes.
–
Jul 24 '14 at 06:52