Using map projections with astronomical data

Question

I noticed that all important "Geoprojections" are available in projections for a spherical reference models: GeoProjectionData function;

1 - I am trying using the sinusoidal projection for astronomical data purposes. I want to use the frames of this projection to plot astronomical points in that map , using right ascension and declination as the coordinates, both in degrees.

In the link below, is a data that can be used, the format is { {RA,DEC, Velociy},....}. Just need the RA, DEC parameters.

DataSample

a. I got the data in {Dec, Ra} :

p = Reverse[#] & /@ rad[[All, {1, 2}]]

b.then I transformed the parameters DEC RA, to sinusoidal numbers:

dat = GeoGridPosition[GeoPosition[p], "Sinusoidal"][[1]]

c. I did the following code:

 GeoListPlot[dat, GeoRange -> All, GeoProjection -> "Sinusoidal", 
 GeoGridLines -> Automatic, 
 GeoGridLinesStyle -> Directive[Dashing[{0.0005, 1 - 0.9950}], Green],
  GeoBackground -> Black, Frame -> True, 
 FrameLabel -> {"RA (\[Degree])", "DEC (\[Degree])"},  
 PlotMarkers -> Style[".", 10, Red]]

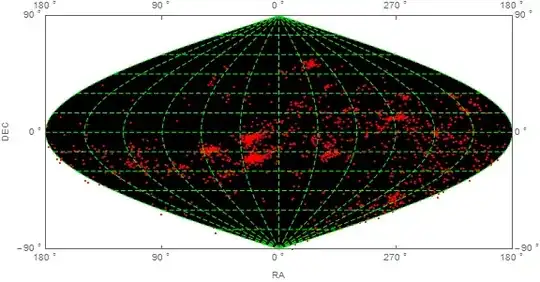
And the resulting plot is:

But no data was plotted.

And the ranges of Frame Axis are wrong: the horizontal axis has to be middle to left 0 90 180, and middle to right 0 (or 360) 270 180.

In the Vertical Axis: -90(bottom) 0(center) +90(top)

EDIT 1:

The link to wolfram math world about sinusoidal projection : Sinusoidal

Answer 1

Edit: for general approach to Ticks, go there: GeoProjection for astronomical data - wrong ticks

---

data = Cases[ Import[FileNames["*.dat"][[1]]],
              {a_, b_, c_} :> {b, Mod[a, 360, -180]}]; (*thanks to bbgodfrey*)

To show points you have to stick with GeoGraphics. GeoListPlot is designed for Entities.

To add something more to the question I changed Ra to hours.

    GeoGraphics[{Red, Point@GeoPosition@data}, 
      GeoRange -> {All, {-180, 180}},
      PlotRangePadding -> Scaled@.01,
      GeoGridLinesStyle -> Directive[Green, Dashed], 
      GeoProjection -> "Sinusoidal", 
      GeoGridLines -> Automatic, 
      GeoBackground -> Black, 
      Axes -> True, 
      ImagePadding -> 25, ImageSize -> 800, 
      Ticks -> {Table[{N[i Degree], Row[{Mod[i/15 + 24, 24]," h"}]}, {i, -180, 180, 30}], 
                Table[{N[i Degree], Row[{i, " \[Degree]"}]}, {i, -90, 90, 15}]}, 
      Background -> Black, 
      AxesStyle -> White, 
      TicksStyle -> 15]

Or change every option with Axes to Frame and:

---

With coloring:

pre = Cases[ Import[FileNames["*.dat"][[1]]], {a_, b_, c_} :> {b, Mod[a, 360, -180], c}];
data = pre[[All, {1, 2}]];
col = Blend[{Yellow, Red}, #] & /@ Rescale[pre[[All, 3]]];



GeoGraphics[{AbsolutePointSize@5, 
  Point[GeoPosition@data, VertexColors -> (col)]}, ...

---

pics = Table[
   GeoGraphics[{AbsolutePointSize@5, 
     Point[GeoPosition[{#, Mod[#2, 360, -180 + t]} & @@@ data], 
      VertexColors -> (col)]}, PlotRangePadding -> Scaled@.01,
    GeoGridLinesStyle -> Directive[Green, Dashed], 
    GeoProjection -> "Bonne", GeoGridLines -> Automatic, 
    GeoBackground -> Black, ImagePadding -> 55, ImageSize -> 400, 
    GeoRange -> "World", GeoCenter -> GeoPosition[{0, t}],
    Background -> Black, FrameStyle -> White, FrameTicksStyle -> 15],
   {t, -180, 170, 5}];

Export["gif.gif", pics, "DisplayDurations" -> 1/24.]

Answer 2

Import data (from wherever it is located):

rad = Import["C:/Temp/DadosRad2014_RADECVELOC_15124_1024.dat"]

Reverse first two elements of each sublist of rad, assure that RA lies in between -180 and 180, and discard third element;

p = Cases[rad, {a_, b_, c_} -> {b, Mod[a, 360, -180]}];

Fix GeoGridLines, adjust ImageSize, and adjust FrameTicks and FrameLabel to reflect that angles are measure in radians:

dat = GeoGridPosition[GeoPosition[p], "Sinusoidal"][[1]];
grid = GeoListPlot[dat, GeoRange -> All, GeoProjection -> "Sinusoidal", 
  GeoGridLines -> Automatic, GeoGridLinesStyle -> Directive[Dashing[{.01, .005}], Green], 
  GeoBackground -> Black, Frame -> True, FrameLabel -> {"RA (rad)", "DEC (rad)"}, 
  PlotMarkers -> Style[".", 10, Red], ImageSize -> Large,
  FrameTicks -> {{-Pi, -Pi/2, 0, Pi/2, Pi}, {-Pi/2, 0, Pi/2}}]

Although, for reasons that are unclear, the data points do not appear on the grid, they can be plotted separately.

data = ListPlot[dat, PlotStyle -> Red, Axes -> False, Frame -> True, 
  FrameLabel -> {"RA (rad)", "DEC (rad)"}, ImageSize -> Large, 
  PlotRange -> {{-Pi, Pi}, {-Pi/2, Pi/2}}, 
  FrameTicks -> {{-Pi, -Pi/2, 0, Pi/2, Pi}, {-Pi/2, 0, Pi/2}}]

Although attempting to directly overlay the two plots with Show generates errors, it is possible to overlay the Graphics Part of grid with data to obtain the desired result. (The order of the two plots in Show matters.)

Show[grid[[1]], data, ImageSize -> Large]

Update

It turns out that GeoListPlot did not display the data points in the procedure above, because GeoPosition is not Listable. This can be overcome by Threading Geoposition over the data points (or Mapping it, as suggested by Kuba in a Comment):

GeoListPlot[Thread[GeoPosition[p]], GeoRange -> All, GeoProjection -> "Sinusoidal", 
 GeoGridLines -> Automatic, GeoGridLinesStyle -> Directive[Dashing[{.01, .005}], Green], 
 GeoBackground -> Black, Frame -> True, FrameLabel -> {"RA", "DEC"}, 
 PlotMarkers -> Style[".", 20, Red], ImageSize -> Large, 
 FrameTicks -> {{{-Pi + .001, Row[{180, " \[Degree]"}]}, {-N[Pi/2], Row[{90, " \[Degree]"}]},
 {0., Row[{0, " \[Degree]"}]}, {0.5 Pi, Row[{270, " \[Degree]"}]}, 
 {Pi - .001, Row[{180, " \[Degree]"}]}}, {{-0.5 Pi, -Row[{90, " \[Degree]"}]}, 
 {0., Row[{0, " \[Degree]"}]}, {0.5 Pi, Row[{90, " \[Degree]"}]}}}]

(The choice of FrameTicks is motivated by one of the OP`s Comments.)