As shown by In1, integrating Sqrt[x^2 - 1]/(a + x^2) (1/x) returns a result with a complex terms; however, after I make a transformation as shown in In2, Mathematica gives a simpler form.
I have no doubt the two outputs are both right and are actually the same thing, but my question is: for the input as given in In1, is there any method that can be applied to the output of In1 that will give the same output as Out2? That is, can the result of In1 be transformed by Mathematica itself into the desired form, thus, making the integration easier?
In1:
Integrate[Sqrt[x^2 - 1]/(a + x^2) (1/x), {x, 1, t}, Assumptions -> t > 1 && a > 5]

In2:
Integrate[Sqrt[y - 1]/(a + y) (1/(2y)), {y, 1, t^2}, Assumptions -> t > 1 && a > 5]


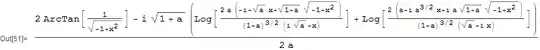


Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign!
– Jan 28 '15 at 05:45