Cutting bagels into linked halves

Question

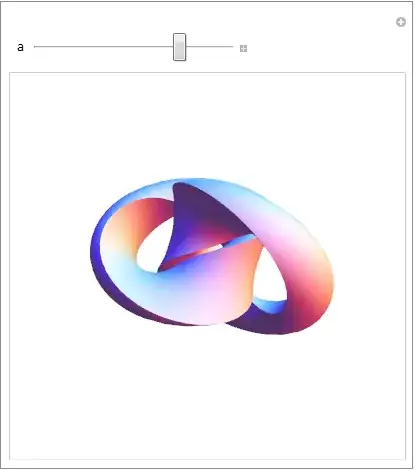
I recently came across this video: Mathematically correct breakfast, which shows how a bagel can be neatly sliced into two identical linked halves.

I'd like to try this with Mathematica. Here's a ~~torus~~ bagel and a ~~Möbius strip~~ cut overlaid. How can I slice the bagel along this cut to create the two halves and pry it open?

With[{opts = {Mesh -> False, Boxed -> False, Axes -> False}},
     bagel = ParametricPlot3D[{Cos[t] (3 + Cos[u]), Sin[t] (3 + Cos[u]), Sin[u]}, 
        {t, 0, 2 Pi}, {u, 0, 2 Pi}, opts, 
        PlotStyle -> Directive[Opacity[0.3], FaceForm[Orange], Lighting -> "Neutral"]];
     cut = ParametricPlot3D[{Cos[t] (3 + r Cos[t/2]), Sin[t] (3 + r Cos[t/2]), r Sin[t/2]}, 
        {r, -1, 1}, {t, 0, 2 Pi}, opts, 
        PlotStyle -> Directive[Opacity[0.9], FaceForm[Gray], Lighting -> "Neutral"]];
]
bagel ~Show~ cut

enter image description here

Although I've used a Möbius strip for the cut, I have a feeling it is a 2-twist strip because of the two sides — I haven't been able to fit this correctly inside a torus...

I saw the image of the bagel and said to myself, "I bet Professor Hart made that.." — BlueRaja - Danny Pflughoeft, Jun 28 '12 at 04:57

score 78 · Accepted Answer · edited Jun 29 '12 at 12:55

Here's one way to slice the donut. To draw one half of the sliced donut I'm using a parameterisation of a torus similar to the one on wikipedia, but with v replaced with u + v and v running from 0 to Pi instead of 2 Pi. This means that the cut is actually a double twist loop.

pl = ParametricPlot3D[{{Sin[u] (2 + Cos[u + v]), Cos[u] (2 + Cos[u + v]), Sin[u + v]},
   {Sin[u] (2 + (2 v/Pi - 1) Cos[u]), Cos[u] (2 + (2 v/Pi - 1) Cos[u]), 
    (2 v/Pi - 1) Sin[u]}}, 
  {u, 0, 2 Pi}, {v, 0, Pi}, Mesh -> False, Boxed -> False, Axes -> False]

Mathematica graphics

We could plot the other half in a similar way but to show that the two halves are identical, you can take pl and rotate it over 180 degrees around the z-axis:

Graphics3D[{pl[[1]], Rotate[pl[[1]], Pi, {0, 0, 1}]}, Boxed -> False]

Mathematica graphics

To pry the two halves open, we need to simultaneously rotate and translate one of the halves, for example

Manipulate[Graphics3D[{pl[[1]], 
   Translate[Rotate[Rotate[pl[[1]], 180 Degree, {0, 0, 1}], -a Degree, {1, 0, 0}], 
  {1.8 a/90, 0, 0}]}, Boxed -> False], 
 {{a, 0}, 0, 90}]

Mathematica graphics

Here's an animation of the process:

enter image description here

As a tiny mathematical note, the derivation of the parametric equations {(c + b Cos[u + v]) Sin[u], (c + b Cos[u + v]) Cos[u], b Sin[u + v]} might be slightly clearer if seen in matrix-vector format: RotationMatrix[-u, {0, 0, 1}].({0, c, 0} + RotationMatrix[u, {1, 0, 0}].{0, b Cos[v], b Sin[v]}) — J. M.'s missing motivation, Jun 28 '12 at 15:18
@Heike, Marvellous!! You could perhaps also animate both ways, slicing, putting back (like after applying butter and jam)! I had earlier played with Villarceau Circles, but this one is more fun...I had also uploaded an image here or in SE Math with a Moebius partition (single twist) without showing opening up rotation of one of the two halves.. — Narasimham, May 18 '16 at 19:04

J. M.'s missing motivation · Answer 2 · 2012-06-30T04:51:27.743

20

(This was supposed to be a comment, but it got a bit too long.)

Heike depicted the "sliced bagel" as a composite of two surfaces. Here's how to plot it as a single surface:

With[{c = 2, b = 1}, 
 ParametricPlot3D[Evaluate[
         RotationMatrix[-u, {0, 0, 1}].({0, c, 0} +
         RotationMatrix[u, {1, 0, 0}].{0, b Cos[v], b UnitStep[Pi - v] Sin[v]})],
                  {u, 0, 2 Pi}, {v, 0, 2 Pi}, Axes -> False, Boxed -> False, Mesh -> False]]

sliced fake bagel

Now if only there was a way to realistically color the "bagel"...

fake bagel?

(If you think that last one is sufficiently "realistic", I'll add the Perlin noise routines needed for this coloring.)

edited Jun 30 '12 at 04:51

answered Jun 29 '12 at 12:25

J. M.'s missing motivation

124,525
11
401
574

That's an everything bagel right there! ;) The inside doesn't look like bready texture though :P – rm -rf Jun 29 '12 at 15:09
Yes, that's going to need some more thought on my end; that's why I didn't post code for the colored version for the time being. (Getting Perlin noise to do what you want can be difficult sometimes...) – J. M.'s missing motivation Jun 29 '12 at 15:13
I'll wait patiently for some Perlin goodness :D – rm -rf Jun 29 '12 at 15:14
I could "toast" the bagel a bit more, if you guys want... or did I do okay with the current shade of brown? – J. M.'s missing motivation Jun 30 '12 at 13:09
The crust can be browned a little more, if only to give more contrast with the bready stuff... One way out of texturing the holes would be to sloppily put perlin cream cheese on it :) – rm -rf Jun 30 '12 at 16:49
2

The appropriately named "Baked Goods" section of my website http://www.maths.ed.ac.uk/~aar/baked/ includes several references to bagel slicing, and in particular a topological analysis of the possible ways of linking/unlinking a bagel, which is related to the Maslov index. – Andrew Ranicki May 05 '15 at 06:03
@ J.M. A thing of beauty.. Gauss curvature somewhere positive, somewhere negative; part of surface is orientable and (sliced) part unorientable ! – Narasimham May 18 '16 at 19:17

Cutting bagels into linked halves

2 Answers2

Linked