Curve wound on torus

Question

I'm beginner in the Mathematica and would like to do some animation based on curve function :

 function = Function[{u, v}, 
  Re[2 Exp[2 \[Pi] I (u + 2 v)] + 6 Exp[2 \[Pi] I (u - 2 v)]]];

After including this curve to the torus pattern :

torus parametric form :

x = Cos[2 Pi v] (2 + Cos[2 Pi u])
y = Sin[2 Pi v] (2 + Cos[2 Pi u])
z = Sin[2 Pi u]

How could I do animation :

• Point moving on this curve
• Winding curve on the torus

Could someone explain me how can i do this ?

Parametric curve form :

u = u(t)
v = v(t)

Answer 1

Ok, lets go step by step. First you want to create a torus. The right parametric form is {Cos[v] (r + Cos[u]), Sin[v] (r + Cos[u]), Sin[u]}.

r = 2;
pl1 = ParametricPlot3D[{Cos[v] (r + Cos[u]), Sin[v] (r + Cos[u]), 
       Sin[u]}, {v, 0, 2 Pi}, {u, 0, 2 Pi}, Mesh -> False,
       PlotStyle -> Opacity[0.7]];

Then you want to make a line on this torus using u=u(t) and v=v(t). I took a trial for u=3t and v=2t.

pl2 =  ParametricPlot3D[Block[{u = 3 t, v = 2 t}, {Cos[v] (r + Cos[u]), 
        Sin[v] (r + Cos[u]), Sin[u]}], {t, 0, 2 Pi}, PlotStyle -> Thick];

Then combine them with Show. The extra point which is supposed to move, you can add as another Graphics3D object whose coordinate will be the animate variable like,

Animate[Show[pl1, pl2, Graphics3D[{Red,
  Sphere[Block[{u = 3 t0, v = 2 t0}, {Cos[v] (r + Cos[u]), 
  Sin[v] (r + Cos[u]), Sin[u]}], 0.1]}]],{t0,0,2 Pi}]

Honestly speaking I don't understand how you want to use the first function, but I guess this can give you a general guide.

And BTW, your function is simply f[x_,y_]=6 Cos[2 Pi x - 4 Pi y] + 2 Cos[2 Pi x + 4 Pi y].

Answer 2

ParametricPlot3D[ {(2 + Cos[ 2 Pi v]) Cos[ 2 Pi u], (2 + Cos[ 2 Pi v]) Sin[2 Pi u], Sin[2 Pi v]}, {v, 0, 1}, {u, 0, 1}]

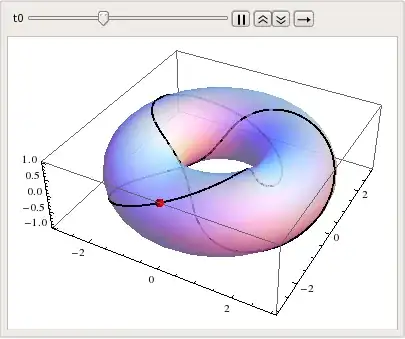
You want to draw certain lines on above torus it appears.

Next,please describe the character of winding lines you choose to depict on it, as that comes at first. For example do you want to draw geodesics? loxodromes? Planar cut loci? Intersection with another surface? or what? Animation can come later on.

$u(t), v(t)$ is not specific enough. The first real part of exponential is not clear. Can you put that the line parametrization into the form:

$$ x(t),y(t),z(t) ? $$

EDIT1:

Geodesics can be found by employing Clairaut's Law

$$ r\cdot \sin \alpha = r_{min}$$

Useful reference

TorusGeodesicsRef

If inner radius is $c$ then there are three possible scenarios for return of running geodesics.

If $ r_{min} < c $ geodesics cover the torus fully, criss crossing but running in same direction.

If $ r_{min} > c $ geodesics cover outside portion only, criss crossing while running to and fro.

If $ r_{min} = c $ geodesics asymptotically reach $ r_{min} = c $ towards an inner torus equator line of no return ... at the torus inner equatorial radius.

EDIT2:

Since you left the choice of type of line to be drawn I chose edge lines of constant width strips. They can be used to wind closely packed copper wires for example on a toroidal solenoid. They are also geodesic parallel lines because separation between them is constant satisfying DE $ r\cdot \cos \alpha = const.$ They are orthogonal trajectories to geodesics.

So Viviani can join Sumit's bandwagon ! ( as $ u=v ?$ )

sph = {Sin[v] Cos[u], -Cos[v] Cos[u], Sin[u]}; 
cyl = {.5 Sin[p], -.5 - .5 Cos[p] , q} 
pl0 = ParametricPlot3D[cyl, {p, 0, 2 Pi}, {q, -1, 1}, Mesh -> False,     PlotStyle -> Opacity[0.3]]; 
pl1 = ParametricPlot3D[sph, {v, 0, 2 Pi}, {u, 0, 2 Pi}, Mesh -> False,
        PlotStyle -> Opacity[0.7]]; 
(* u=v=t for Viviani_Curve *) 
pl2 = ParametricPlot3D[Block[{u = t, v = t}, sph], {t, 0, 2 Pi}, PlotStyle -> Thick]; 
Animate[Show[pl1, pl0, pl2,    Graphics3D[{Red, Sphere[Block[{u = tz, v = tz}, sph], 0.04]}]], {tz,    0, 2 Pi}]