1

I have the 3d cone:

Plot3D[-Sqrt[x^2 + y^2], {x, -20, 20}, {y, -20, 20}, Mesh -> None, 
 BoxRatios -> {1, 1, 1}]

I need a slanted plane intersecting it. Can somebody help me?

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
marle
  • 145
  • 1
  • 7
  • 2
    Add a plane to your plot? e.g. Plot3D[{-Sqrt[x^2 + y^2], -1 - x - y}, {x, -1, 1}, {y, -1, 1}] – 2012rcampion Feb 26 '15 at 00:10
  • 1
    I don't quite get what you're after. You know the equation of a cone but not of a plane? Any linear function of x and y yields a plane. – Michael E2 Feb 26 '15 at 00:19

2 Answers2

3
Graphics3D[
 {
  {Opacity[0.5], Cone[{{0,0,0}, {0,0,3}}, 1]},
  {Yellow, Opacity[0.5], Polygon[{{-1,-1,1}, {-1,1,1}, {1,1,2}, {1,-1,2}, {-1,-1,1}}]}
  }
 ]

enter image description here

Or play around with this:

Manipulate[
 Graphics3D[
  {
   {LightBlue, Opacity[0.5], Cone[{{0, 0, 0}, {0, 0, 3}}, rcone]},
   {Yellow, Opacity[0.5], 
    Polygon[{{-1,-1,1}, {-1,1,1}, {1,1,m}, {1,-1,m}, {-1,-1,1}}]}
   }
  ],
 {rcone, .5, 2}, {m, 1, 3}
 ]
David G. Stork
  • 41,180
  • 3
  • 34
  • 96
2

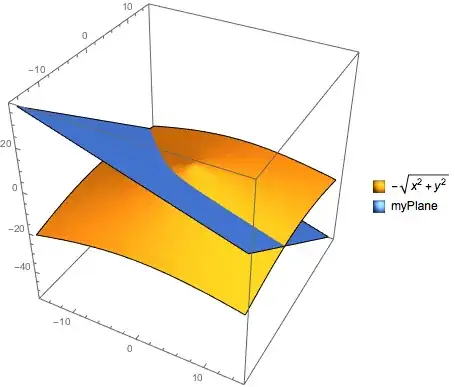
let's say you have a plane:

myPlane=-8-x-2y

you can use Plot3D like so;

Plot3D[{-Sqrt[x^2 + y^2], myPlane}, {x, -15, 15}, {y, -15, 15}, 
Mesh -> None, BoxRatios -> {1, 1, 1}, PlotLegends -> "Expressions"]

enter image description here

you can pimp your plot with RegionFunction:

Plot3D[{-Sqrt[x^2 + y^2], myPlane}, {x, -15, 15}, {y, -15, 15}, 
 RegionFunction -> Function[{x, y, z}, -10 < z < 10], BoxRatios -> 1, 
 PlotLegends -> "Expressions"]

enter image description here

and or and specify ViewPoint for visualization:

enter image description here