Plot3D[{-5 - x - y, -Sqrt[8 x^2 + 8 y^2]}, {x, -5, 5}, {y, -5, 5},
Mesh -> None, BoxRatios -> {1, 1, 1}, PlotLegends -> "Expressions"]
Asked
Active
Viewed 603 times
4
marle
- 145
- 1
- 7
-
You could use Solve to find the equation of the intersection and then use ParametricPlot3D to plot it. Combine it with the other plot using Show. – Sjoerd C. de Vries Mar 18 '15 at 18:51
-
Alternatively, you could use RegionIntersection with Cone and InfinitePlane. – Sjoerd C. de Vries Mar 18 '15 at 18:56
-
possible duplicate of About Slicing through Graphics3D – Jens Mar 18 '15 at 19:13
-
@jens It is my impression (but I may be wrong here) that the OP wants to see the plane and cone and their intersection (accentuated). The post you referred to has the plane slice off a piece of the cone, which is not the same. – Sjoerd C. de Vries Mar 18 '15 at 20:55
-
@SjoerdC.deVries I'd suggest the OP clarify the question so as to not waste time with misinterpretations... – Jens Mar 18 '15 at 21:07
-
@jens That would indeed be better. I just noted that the question is a follow-up of this one. It suggests that what is needed is the outline of the intersection, but who knows? – Sjoerd C. de Vries Mar 18 '15 at 21:13
-
Duplicate: http://mathematica.stackexchange.com/questions/75917/a-cone-being-intercepted-by-a-slanted-plane – David G. Stork Mar 18 '15 at 21:15
-
@DavidG.Stork Did you read the comments above (and the question)? – Sjoerd C. de Vries Mar 18 '15 at 21:41
-
1To the closers: The OP has update the question to indicate that she wants the outline of the intersection be marked. This is not the case in the question linked as duplicate. – Sjoerd C. de Vries Mar 18 '15 at 22:38
2 Answers
9
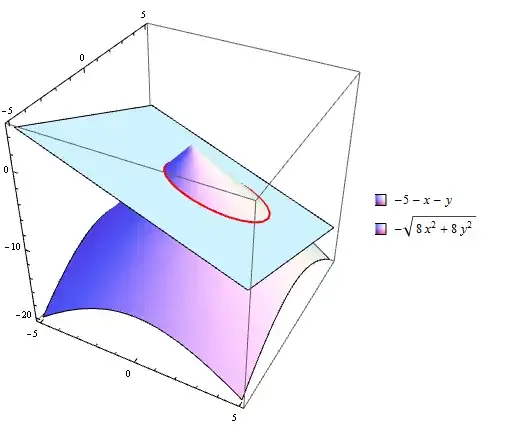
Using BoundaryStyle
Use the option BoundaryStyle and set the option value to {{1, 2} -> Directive[Thick, Red]}:
Plot3D[{-5 - x - y, -Sqrt[8 x^2 + 8 y^2]}, {x, -5, 5}, {y, -5, 5},
Mesh -> None, BoxRatios -> {1, 1, 1},
BoundaryStyle -> {{1, 2} -> Directive[Thick, Red]} ]
Note: This particular usage for BoundaryStyle in not documented. The earliest reference on this site is this answer by Daniel Lichtblau
Using MeshFunctions
Use the difference between the two functions as the setting for option MeshFunctions:
Plot3D[{-5 - x - y, -Sqrt[8 x^2 + 8 y^2]}, {x, -5, 5}, {y, -5, 5},
MeshFunctions -> {-5 - # - #2 - (-Sqrt[8 #^2 + 8 #2^2]) &},
Mesh -> {{{0, Directive[Red, Thick]}}}, BoxRatios -> {1, 1, 1},
PlotLegends -> "Expressions"]
-
+1 Of course. Interestingly, your specific application of BoundaryStyle does not seem to be documented on its documentation page. Where did you learn about this? – Sjoerd C. de Vries Mar 19 '15 at 13:28
-
@SjoerdC.deVries, thanks for the vote. It is not in documentation. I have a faint memory of having seen something like this on this site; but i could not find it with the usual key words. Btw, it does not work in some cases where one would wish it would, e.g. i could not find a way to make it work in [this q/a[(http://mathematica.stackexchange.com/q/58045/125) – kglr Mar 19 '15 at 13:45
-
-
Ah, that's great! I see that I voted for it, so I should have known. – Sjoerd C. de Vries Apr 14 '15 at 22:09
6
Find equations for intersection:
Solve[-5 - x - y == -Sqrt[8 x^2 + 8 y^2], x]
{{x -> 1/7 (5 + y - 2 Sqrt[2] Sqrt[25 + 10 y - 6 y^2])}, {x -> 1/7 (5 + y + 2 Sqrt[2] Sqrt[25 + 10 y - 6 y^2])}}
Range of y:
Solve[25 + 10 y - 6 y^2 == 0, y]
{{y -> 5/6 (1 - Sqrt[7])}, {y -> 5/6 (1 + Sqrt[7])}}
Draw intersection:
inter =
With[
{
x1 = 1/7 (5 + y - 2 Sqrt[2] Sqrt[25 + 10 y - 6 y^2]),
x2 = 1/7 (5 + y + 2 Sqrt[2] Sqrt[25 + 10 y - 6 y^2])
},
ParametricPlot3D[{{x1, y, -5 - x1 - y}, {x2, y, -5 - x2 - y}},
{y, 5/6 (1 - Sqrt[7]), 5/6 (1 + Sqrt[7])},
PlotStyle -> Blue
]
]
Add other objects:
cone = Cone[{{0, 0, -Sqrt[200]}, {0, 0, 0}}, 5];
plane = InfinitePlane[{{0, 0, -5}, {-5, 0, 0}, {0, -5, 0}}];
Show[
Graphics3D[{Opacity[0.8], cone, plane}],
inter
]
Sjoerd C. de Vries
- 65,815
- 14
- 188
- 323