8

I want to solve diffusion of a point source numerically and check it against analytical solution. first I define initial profile,

ClearAll["Global`*"];
deltaPos = 0;
InitComp = 100;
g[x_] := Piecewise[{{0, x < deltaPos}, {100, x == deltaPos}, {0, 
    x > deltaPos}}]

and the solve the differential equation,

pde = D[u[x, t], t] - 0.2 D[D[u[x, t], {x, 1}], {x, 1}] == 0;
sol = NDSolve[{pde, u[x, 0] == g[x], u[-10, t] == 0, u[10, t] ==0}, 
   u[x, t], {x, -10, 10}, {t, 0, 20}];

Now, I expect that total mass of the system is essentially conserved, since diffusion is yet to reach boundary points. Initial mass of the system is

NIntegrate[u[x, t] /. sol /. {t -> 0}, {x, -10, 10}]

which outputs $0$, which is acceptable since total mass is concentrated at a single point. Now to check mass after some time(essentially any time t=0.0001,0.1,1,10), 

NIntegrate[u[x, t] /. sol /. {t -> 1}, {x, -10, 10}]

outputs to $0.2$, which is confusing. I think integration should produce $100$, which is the total initial mass of the system.

Analytical solution after time t is (with $ D = 0.2, C_0 = 100$), \begin{eqnarray} f(x,t) = \frac{C_0}{\sqrt{4\pi Dt}}\exp\left(\frac{-x^2}{4Dt}\right) \end{eqnarray}

Comparing the results with analytical solution,

AnaS[x_] := 100*Exp[-x*x/(4*0.2*10)]/(Sqrt[4*3.14159265*0.2*10])
Plot[AnaS[x], {x, -10, 10}]
Plot[u[x, t] /. sol /. {t -> 10}, {x, -10, 10}]

tells that numerical solution is off by exactly factor of $500$. What am I missing here? Also another question regarding the boundary conditions. How can set boundary conditions like $\frac{\partial u}{\partial x} = 0$ at the boundaries? I tried

D[u[10,t],x]==0

but it did not work.

xzczd
  • 65,995
  • 9
  • 163
  • 468
alekhine
  • 429
  • 2
  • 7
  • 2
    I don't think your way of defining a point source is correct. The peak has a finite height but a width of zero, so it basically contains nothing. – Sjoerd C. de Vries Apr 29 '15 at 11:20
  • @SjoerdC.deVries, I know in c++, this way of defining point source works just fine. I am not sure with Mathematica. – alekhine Apr 29 '15 at 11:23
  • You mean: "a program you know, that has been written in C++, works in a way that it can handle peaks in the way you defined", right? You realize that that has nothing to do with C++ itself, do you? – Sjoerd C. de Vries Apr 29 '15 at 11:28
  • I meant any code using finite difference method to solve the differential equation should be able to handle the pick in the way defined above as intended. Nothing specific to C++, but I do not know how Mathematica handles this. – alekhine Apr 29 '15 at 11:33
  • Your InitComp parameter is never used. The factor 500 is 100/0.2. – b.gates.you.know.what Apr 29 '15 at 11:49
  • @bobthechemist, for $n$ dimensions, coefficient before exponential function is $\frac{1}{(4\pi D t)^{n/2}}$. here $n=1$ – alekhine Apr 29 '15 at 11:51
  • 1
    Related: http://mathematica.stackexchange.com/a/71945/1871 – xzczd Apr 29 '15 at 11:53
  • 2
    the boundary conditions for x=-10 and x=10 are completely invalid. A peculiarity of the diffusion equation is that perturbations propagate instantaneously. Another thing is the way, your "delta-function" is defined. NDSolve gives an message that it is looking at 10000 grid points for x. The interval for x is {-10,10} thus it might mistakenly interpret the single point of g[x]=100 as a peak of width around 0.002 and height up to 100 giving a total mass of around 0.2 (500 smaller than the desired 100. If I increase the x range to {-20,20} the solution becomes twice as large. – LLlAMnYP Apr 29 '15 at 15:02
  • 2
    @alekhine, I meant any code using finite difference method . This requires, that a) deltaPos is among the sampling points, b) the effective mass you'll get is dependent on the density of the sampling points. – LLlAMnYP Apr 29 '15 at 16:27

1 Answers1

8

The reason why you get a factor of 500 of I have explained in my comment. Let's replace your g with a better behaved function:

mass = 100;
width = 10^-2;
g[x_] := mass/width HeavisideLambda[x/width]

This is a triangular peak with area 100 and basewidth 0.01.

Now let's impose the desired boundary conditions of $\partial u / \partial x =0$ at the boundaries:

Derivative[1, 0][u][-10, t] == 0
Derivative[1, 0][u][10, t] == 0

Now back to your code:

pde = D[u[x, t], t] - 0.2 D[D[u[x, t], {x, 1}], {x, 1}] == 0;
sol = NDSolve[{pde, u[x, 0] == g[x], Derivative[1, 0][u][-10, t] == 0, 
   Derivative[1, 0][u][10, t] == 0}, u[x, t], {x, -10, 10}, {t, 0, 20}]

This will of course complain due to the absence of a continuous derivative (much less, a continuous second derivative) of g[x], but it will come up with something.

Plot3D[u[x, t] /. sol, {x, -5, 5}, {t, 0, 20}, PlotRange -> Full]

Initial conditions

Huge peak at the beginning (just a finite approximation of a delta-function).

Plot3D[u[x, t] /. sol, {x, -10, 10}, {t, 0, 20}]

Development

Something saner, as diffusion takes place.

{-10, 10} is quite a large box. It's hard to see, that the process of diffusion is really contained within it. Let's confine the region a bit and give more time to develop.

sol = NDSolve[{pde, u[x, 0] == g[x], Derivative[1, 0][u][-3, t] == 0,
    Derivative[1, 0][u][3, t] == 0}, u[x, t], {x, -3, 3}, {t, 0, 50}]
Plot3D[u[x, t] /. sol, {x, -3, 3}, {t, 0, 30}, PlotRange -> {0, 30}]

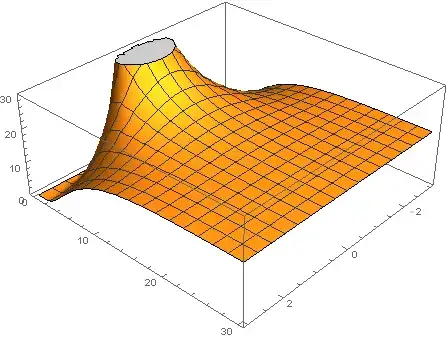
Levelling off

Now the peak fills the box up to about 15.

NIntegrate[u[x, t] /. (First@sol) /. t -> 0, {x, -0.1, 0.1}]

100.08

I've chosen this range, because at t=0 the peak is a bit narrow and NIntegrate can miss it.

Let's check, how everything evolves with time:

Do[Print[NIntegrate[u[x, t] /. (First@sol) /. t -> tt, {x, -3, 3}]],
   {tt, {1, 5, 10, 20, 30, 40}}]

100.08
100.08
100.08
100.08
100.08
100.08

Very consistent. But I don't like the 0.08 error. Let's try to make NDSolve's job a bit easier by specifying easier initial conditions (broader peak, so numerical precision isn't so much of an issue).

mass = 100;
width = 1;
g[x_] := mass /width HeavisideLambda[x/width]
sol = NDSolve[{pde, u[x, 0] == g[x], Derivative[1, 0][u][-3, t] == 0, 
   Derivative[1, 0][u][3, t] == 0}, u[x, t], {x, -3, 3}, {t, 0, 50}]
Do[Print[NIntegrate[u[x, t] /. (First@sol) /. t -> tt, {x, -3, 3}]],
   {tt, {1, 5, 10, 20, 30, 40}}]

100.
100.
100.
100.
100.
100.

EDIT follow-up for ill-defined peak functions :-)

Clear[g]; deltaPos = 0; 
g[x_] := Piecewise[{{0, x < deltaPos}, {100, x == deltaPos}, {0, x > deltaPos}}]
pde = D[u[x, t], t] - 0.2 D[D[u[x, t], {x, 1}], {x, 1}] == 0;
sol = NDSolve[{pde, u[x, 0] == g[x], Derivative[1, 0][u][-10, t] == 0,
    Derivative[1, 0][u][10, t] == 0}, u[x, t], {x, -10, 10}, {t, 0, 50}]
Plot3D[u[x, t] /. sol, {x, -3, 3}, {t, 0.1, 3}, PlotRange -> Full]

produces this (below), as x=0 is included in the initial sampling points.

Lucky us

Naturally, NDSolve complains about reaching the maximum of allowed grid points, because it detects a peak in g[x], but can't get a handle on how narrow it is:

NDSolve::mxsst: Using maximum number of grid points 10000 allowed by the MaxPoints or MinStepSize options for independent variable x. 

Clear[g]; deltaPos = 2; 
g[x_] := Piecewise[{{0, x < deltaPos}, {100, x == deltaPos}, {0, x > deltaPos}}]

With a definition like above NDSolve shuts up and returns u[x, t] that is zero across the domain. The initial sampling grid seems to be rather coarse. It simply doesn't realize, that there's an out-of-place peak in your starting function. deltaPos = 5 is, however, among the sampling points. That returns a much saner result, similar to what we get for deltaPos = 0. The lesson to learn is "define your point sources properly".

Thanks for asking the question, it brought a great deal about solving ODEs with Mathematica to my attention, especially in the linked question in the comments.

LLlAMnYP
  • 11,486
  • 26
  • 65