How do I draw random points from a region

Question

as the title,this problem have confused me a whole day.If I have a region,how can I yield a random member in this region.The region such as Triangle[{{0, 0}, {1, 2}, {2, 1}}]or (x>5&&x<9)||(x>11&&x<13)

i want get a random member in the expected region.but the “FindInstance” will give me a same result in the scond time when i run it again.

my current solution is previously product some random member,then sift that expected that.but the way will result in a long time,because it has yield amounts of member that it don't meet the requestion.

@Simon Woods yeah,i had tried it today.I think i should revise my quetion,i want get a random member in the expected region.but the FindInstance will give me a same result in the scond time when i run it again. — yode, May 09 '15 at 15:28
Have you seen this? An adaptation to Mathematica ought to be straightforward. — J. M.'s missing motivation, May 09 '15 at 15:41
One thing you could do would be to use the optional fourth argument of FindInstance and find many points all at once. Then use these one by one. — bill s, May 09 '15 at 16:02
You can triangulate any polygonal region, yes? Pick any of those triangles at random (use RandomChoice[] with the triangle areas as weights), then use the triangle point picking strategy. — J. M.'s missing motivation, May 09 '15 at 16:05
I don't have the latest version of Mathematica to confirm, but version 8 had nice goodies under the Graphics`Mesh` context; PolygonTriangulate[] and PolygonArea[] are particularly relevant. — J. M.'s missing motivation, May 09 '15 at 16:46

score 5 · Answer 1 · edited Apr 13 '17 at 12:19

5

Following the advice of @Guess who it is. to use https://math.stackexchange.com/questions/18686/uniform-random-point-in-triangle

randPt[tri_Triangle] :=
  Module[{a, b, c,
    r1 = Sqrt[RandomReal[]], r2 = RandomReal[]},
   {a, b, c} = Identity @@ tri;
   (1 - r1)*a + r1*(1 - r2)*b + r1*r2*c];

triangle = Triangle[RandomReal[{0, 5}, {3, 2}]]

Triangle[{{4.22625, 2.64524}, {0.95047, 2.79426}, {2.89314, 1.00168}}]

Manipulate[
 Graphics[{
   LightGray, triangle,
   Red, AbsolutePointSize[3],
   Point[Table[randPt[triangle], {n}]]},
  Frame -> True],
 {{n, 500}, 100, 10000, 100, Appearance -> "Labeled"}]

enter image description here

edited Apr 13 '17 at 12:19

Community

1

answered May 09 '15 at 16:36

Bob Hanlon

157,611
7
77
198

Would've used Dot[] myself: {1 - r1, r1 (1 - r2), r1 r2}.{a, b, c}. – J. M.'s missing motivation May 09 '15 at 16:42
…and with that, a definition pattern like randPt[Triangle[pts_?MatrixQ]] := (* stuff *) is useful as well. – J. M.'s missing motivation May 09 '15 at 16:49
@Guesswhoitis. - Yes Dot would be better and faster. – Bob Hanlon May 09 '15 at 16:49
I suggest using argument destructuring to improve randPt. That is, writing it as randPt[Triangle[a_, b_, c_]] := Module[{r1 = Sqrt[RandomReal[]], r2 = RandomReal[]}, (1 - r1)*a + r1*(1 - r2)*b + r1*r2*c] – m_goldberg May 09 '15 at 19:35

score 2 · Answer 2 · edited Apr 13 '17 at 12:55

The general 2D case was discussed in this question, but a more robust version can be written

randomFromRegion2D[
    region_ /; RegionDimension[region] == 2, 
    trials_Integer /: trials > 0] :=
  Module[{bounds, randPts},
    bounds = RegionBounds @ region;
    randPts = 
      Transpose @ 
        {RandomReal[bounds[[1]], trials], RandomReal[bounds[[2]], trials]};
    Select[randPts, RegionMember[region]]]

tri = Triangle[{{0, 0}, {1, 2}, {2, 1}}];
SeedRandom[1]; 
Graphics[{{GrayLevel[.75], tri}, Point @ randomFromRegion2D[tri, 1000]}]

triangle

However, the OP also asked about 1D regions such a one characterized by

(x > 5 && x < 9) || (x > 11 && x < 13)

I would like to discuss how handle such regions, which must be dealt with a little differently than 2D regions because the functions supporting regions in Mathematica insist that points in 1D regions be represented by a list containing a single numeric object. Thus, the 1D origin is {0.}.

The OP's 1D specification can be made into a Mathematica region by taking the union of two Interval objects.

rx = RegionUnion[Interval[{5, 9}], Interval[{11, 13}]]]

randomFromRegion1D[
    region_ /; RegionDimension[region] == 1, 
    trials_Integer /: trials > 0] :=
  Module[{bounds, randPts},
    bounds = RegionBounds @ region;
    randPts = RandomReal[bounds[[1]], {trials, 1}];
    Select[randPts, RegionMember[region]] // Flatten]

SeedRandom[1]; 
NumberLinePlot[randomFromRegion1D[rx, 50],
  Prolog -> {GrayLevel[.75], AbsoluteThickness[10], 
    Line[Transpose @ {rx[[1, 1]], {0, 0}}], 
    Line[Transpose @ {rx[[2, 1]], {0, 0}}]}]

intervals

kglr · Accepted Answer · 2015-05-09T22:08:34.517

You can also use the function Graphics`Mesh`GenerateUniformPointsInTriangle

gupiTriF = Graphics`Mesh`GenerateUniformPointsInTriangle;

Graphics[{Polygon[{{0, 0}, {0, 1}, {1, 0}}], White, Point[gupiTriF@500]}]

Mathematica graphics

For an arbitrary triangle tri you can use FindGeometricTransform to map the random points in the unit right triangle to points in tri:

fgt2DF = FindGeometricTransform[#, {{0, 0}, {1, 0}, {0, 1}}][[2]] &;

SeedRandom[1]
Row[Table[coords = RandomReal[{0, 5}, {3, 2}];
  Graphics[{Hue[RandomReal[]], Polygon@coords, 
      RGBColor[RandomReal[1, {3}]], Point[fgt2DF[coords]/@
         gupiTriF[RandomInteger[{100, 500}]]]}, 
      ImageSize -> 200], {5}]]

enter image description here

Similarly, in 3D, Graphics`Mesh`GenerateUniformPointsInTetrahedron does what its name says:

gupiTetF = Graphics`Mesh`GenerateUniformPointsInTetrahedron;
Graphics3D[{Opacity[.5], EdgeForm[], 
  Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {0, 0, 1}, {0, 1, 0}}], Red,
  Point[gupiTetF@1000]}]

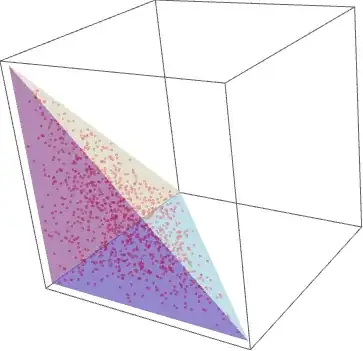
Mathematica graphics

For a random tetrahedron, you can use a geometric transformation similar to the 2D case:

fgt3DF = FindGeometricTransform[#, {{0, 0, 0}, {1, 0, 0}, {0, 0, 1}, {0, 1, 0}}][[2]]&;

SeedRandom[111]
Row[Table[coords = RandomReal[{5, 10}, {4, 3}];
  Graphics3D[{Hue[RandomReal[]], FaceForm[Opacity[.25]], 
    Tetrahedron@coords, RGBColor[RandomReal[1, {3}]],
    Point[fgt3DF[coords] /@ gupiTetF[RandomInteger[{100, 500}]]]}, 
   ImageSize -> 300, Boxed -> False], {3}]]

enter image description here

How do I draw random points from a region

3 Answers3