Why aren't these additions of integrals and summations equal?

Question

I have the following code:

 Simplify[Integrate[f[x] + g[x], x] == Integrate[f[x], x] + Integrate[g[x], x]]

To test:

$$\int{\left(f(x) + g(x)\right)dx}=\int{f(x)dx}+\int{g(x)dx}$$

Why doesn't this simplify to True? More importantly, how can I get this to evaluate to True? I'm going through some manipulations of equations, and I'd like to use Mathematica to doublecheck my math and help with it.

I run into the same problem with Sum, where Integrate in the previous equation can be replaced by Sum. I'm using Mathematica 8.0.4.0.

I found that adding d[expression ,x] with Simplify or FullSimplify will evaluate to true. In other words, I am taking the derivative of the expression, and that seems to eliminate the integrals. I'd like to know if there are other workarounds, though. The new code is: FullSimplify[ D[Integrate[a[x] + b[x], x] == Integrate[a[x], x] + Integrate[b[x], x], x]] — Matt Groff, Jul 15 '12 at 22:56
Why do you need any workarounds ? Your last issue with FullSimplify is just an inconsequence of M. Look at Integrate[a[x] + b[x], x], Integrate[a[x], x] and, all they return the results as the integrals would actually exist, moreover as they would be differentiable. While that is not correct in general. — Artes, Jul 16 '12 at 00:40
@Artes: I was just wondering if there are any related features available. What did you mean by M? — Matt Groff, Jul 16 '12 at 02:03
M like Mathematica. I meant it wasn't a good feature of M when it returned True in that case. Look that you need not FullSimplify to get True, evaluate that expression without FullSimplify. It shouldn't return True, unless you assume a[x] to be integrable/ differentiable e.g. a[x_]:=x^2. There are many imperfect issues. — Artes, Jul 16 '12 at 02:14

Artes · Accepted Answer · 2012-07-19T12:00:06.593

There is nothing wrong with the issue in the question.

Mathematica shouldn't evaluate

Simplify[ Integrate[f[x] + g[x], x] == Integrate[f[x], x] + Integrate[g[x], x]]

to True, because in general such a rule would be mathematically simply wrong.

Consider e.g. $ \forall_{x } f(x) = - g(x)$, while $f$ is not e.g. Lesbegue integrable. Of course Mathematica does not distinguish integrability subtleties, nevertheless there should be

Integrate[f[x] + g[x], x] == 0

while $\int{f(x)dx}$ and $\int{g(x)dx}$ don't not exist. Q.E.D

One should emphasize that the rule works well if we define appropriate integrable functions, e.g.

f[x_] := x^3 + 2 x + 1
g[x_] := Hypergeometric1F1[3, 7, x]
Simplify[ Integrate[ f[x] + g[x], x] == Integrate[ f[x], x] + Integrate[ g[x], x]]

True

Edit

If there is a need for a rule distributing integrals over a sum of functions (knowing that we can do this in an appropriate class of functions) we could define an adequate rule, e.g.

intRule = Integrate[a_ + b_, c_] :> Integrate[a, c] + Integrate[b, c];

and use it with ReplaceRepeated (//.)

( Integrate[ f[x] + g[x] + h[x], x] //. intRule ) == 
  Integrate[f[x], x] + Integrate[g[x], x] + Integrate[h[x], x]

True

in the traditional form it yields :

Integrate[ f[x] + g[x] + h[x], x] //. intRule // TraditionalForm

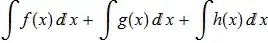
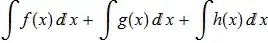
enter image description here

score 9 · Answer 2 · answered Jul 16 '12 at 08:31

To get the behaviour you want, you can tell Simplify to try distributing Integrate over Plus as one of its transformations:

Simplify[Integrate[f[x] + g[x], x] == Integrate[f[x], x] + Integrate[g[x], x], 
 TransformationFunctions -> {Automatic, # /. i_Integrate :> Distribute[i] &}]

True

Why aren't these additions of integrals and summations equal?

2 Answers2

Linked

Related