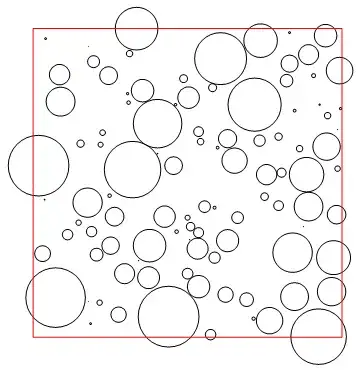
centers = RandomReal[{0, 10}, {20, 2}];
radii = RandomReal[{0, 1}, 20];
Graphics[{MapThread[{RGBColor@@RandomReal[{0, 1}, 3], Circle@##} &, {centers, radii}],
FaceForm[Transparent], EdgeForm[Red],
Polygon[{{0, 0}, {0, 10}, {10, 10}, {10, 0}, {0, 0}}]}]

Edit
If you want disjoint circles you may go with something like:
SeedRandom[42];
f := {RandomReal[{0, 10}, 2], RandomReal[{0, 1}]}
l = {f};
While[
Length@l < 100,
While[k = f;
Not[And @@ ((# + k)[[2]] < EuclideanDistance[#[[1]], k[[1]]] & /@ l)]];
AppendTo[l, k]];
Graphics[{Circle @@@ l, FaceForm[Transparent], EdgeForm[Red],
Polygon[{{0, 0}, {0, 10}, {10, 10}, {10, 0}, {0, 0}}]}]