The following code is faster, but has its own problems. That is, for some settings of the radius bounds it is impossible to fit a large number of disks into the square. In addition, there are fewer tangent points than in the answer by @DavidGStork; however, every disk is tangent to at least one other.
The radius of a new disk is the minimum of the distances to all disk centres minus the disk radii. If the minimum is negative then the new centre lies within an existing disk.
MinCircleRadius[newCentre_List, circles_List] :=
Min[Map[Norm[newCentre - #] &, circles[[All, 1]]] - circles[[All, 2]]]
Find a new disk with radius between rlo and rhi, within a square of side 10, centred on the origin.
FindNewCircle[circles_, rlo_, rhi_] :=
Block[{c = RandomReal[{-5., 5.}, 2], r},
While[(r=MinCircleRadius[c, circles])<rlo || r>rhi, c=RandomReal[{-5.,5.},2]];
{c, r}]
Place disks.
PackSomeCircles[n_, rlo_, rhi_] :=
Nest[Flatten[{#, {FindNewCircle[#, rlo, rhi]}}, 1] &,
{{RandomReal[{-4, 4}, 2], RandomReal[{rlo, rhi}]}}, n]
Begin with a small lower bound to avoid impossible fits.
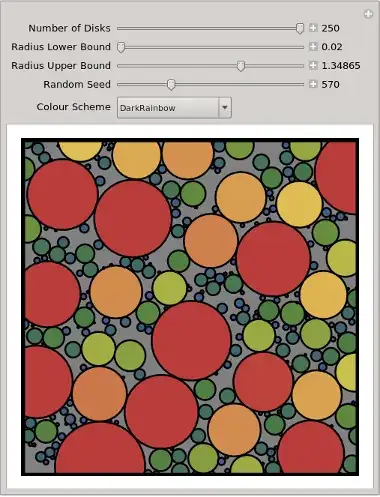
Manipulate[
Module[{c},
SeedRandom[seed];
c = PackSomeCircles[n, rlo, rhi];
Graphics[{
EdgeForm[{Thick, Black}],
Map[{ColorData[cs, #[[2]]], Apply[Disk, #]} &, c],
Thickness[0.02], Line[{{-5,-5}, {5,-5}, {5,5}, {-5,5}, {-5,-5}}]
}, Background -> Gray, PlotRange -> 5 {{-1, 1}, {-1, 1}}]],
{{n, 100, "Number of Disks"}, 2, 250, 1, Appearance -> "Labeled"},
{{rlo, 0.02, "Radius Lower Bound"}, 0.02, 0.99*rhi, Appearance -> "Labeled"},
{{rhi, 1.0, "Radius Upper Bound"}, 1.01*rlo, 2.0, Appearance -> "Labeled"},
{{seed, 1, "Random Seed"}, 1, 2000, 1, Appearance -> "Labeled"},
{{cs, "DarkRainbow", "Colour Scheme"}, ColorData["Gradients"]}]
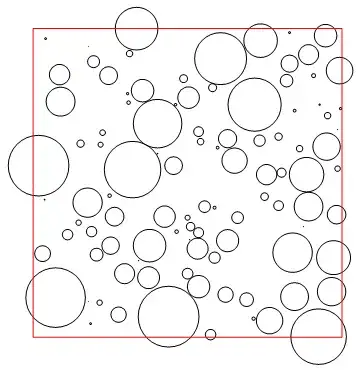


Graphics[{{Hue[RandomReal[]], #} & /@ (Circle @@@ l), FaceForm[Transparent], EdgeForm[Red], Polygon[{{0, 0}, {0, 10}, {10, 10}, {10, 0}, {0, 0}}]}]– David G. Stork Jul 06 '15 at 23:19PlotRange -> {{-.02, 10.02}, {-.02, 10.02}}– David G. Stork Jul 06 '15 at 23:25