Is there an easy way to put time ticks on a parametric plot?

Question

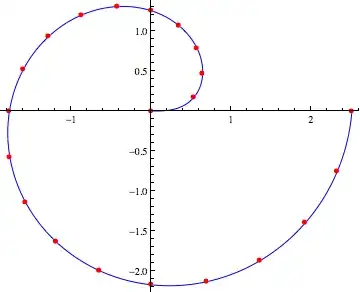
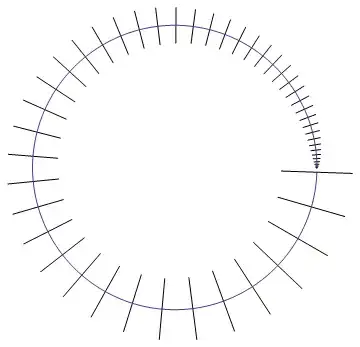
I have a parametric plot showing a path of an object in x and y (position), where each is a function of t (time), on which I would like to put a time tick, every second let's say. This would be to indicate where the object is moving fast (widely spaced ticks) or slow (closely spaced ticks). Each tick would just be short line that crosses the plot at that point in time, where that short line is normal to the plotted curve at that location.

I'm sure I can figure out a way to do it using lots of calculations and graphics primitives, but I'm wondering if there is something built-in that I have missed in the documentation that would make this easier.

(Note: this is about ticks on the plotted curve itself -- this doesn't have anything to do with the ticks on the axes or frame.)

Thanks. Mesh gets close to what I want. If the parametric plot range is {t,a,b}, then it appears I can use Mesh->Round[(b-a)/10] to get dots every 10 seconds. (Obviously it works best if b-a is a multiple of 10.) Now I need to figure out how to turn those into perpendicular line segments. I see that I can set Mesh to a list of tick locations each with a graphics directive ... — Mark Adler, Jul 24 '12 at 23:15

rm -rf · Accepted Answer · 2012-07-24T23:27:45.490

11

To create the ticks perpendicular to the curve, I calculate the direction of the normal to the curve where the ticks are to be placed and then orient a line segment along that direction. The following code does that.

ClearAll[ParametricTimePlot]
SetAttributes[ParametricTimePlot, HoldAll]
ParametricTimePlot[fun_, {var_, min_, max_, steps_}, len_, 
    opts : OptionsPattern[]] := 
    Show[
        ParametricPlot[fun, {var, min, max}, opts],
        Graphics[
            Rotate[Translate[Line[{{-len/2, 0}, {len/2, 0}}], #1], ArcTan @@ #2]
        ] & @@@ (N@Table[{fun, RotationMatrix[π/2].D[fun, var]} /. var -> i, 
            {i, min + steps, max, steps}])
    ]

Use the above function as:

ParametricTimePlot[{ Sqrt[t] Cos[t], Sqrt[t] Sin[t]}, {t, 0, 2 π, 
    π/10}, 0.1, PlotStyle -> Blue]

enter image description here

If you want to keep it simple and just show the dots, then this is very straightforward:

ClearAll[ParametricTimePlot]
SetAttributes[ParametricTimePlot, HoldAll]
ParametricTimePlot[fun_, {var_, min_, max_, steps_}, opts : OptionsPattern[]] :=     
    ParametricPlot[fun, {var, min, max}, opts] 
    ~Show~
    ListPlot[Table[fun /. var -> i, {i, min, max, steps}], 
        PlotStyle -> Red, PlotMarkers -> {Automatic, 8}]

ParametricTimePlot[{ Sqrt[t] Cos[t], Sqrt[t] Sin[t]}, {t, 0, 2 Pi, Pi/10}, 
    PlotStyle -> Blue]

enter image description here

edited Jul 24 '12 at 23:27

answered Jul 24 '12 at 23:05

rm -rf

88,781
21
293
472

1

There's a more compact way to do your second routine. Witness ParametricPlot[{Sqrt[t] Cos[t], Sqrt[t] Sin[t]}, {t, 0, 2 Pi}, Mesh -> {Range[0, 2 Pi, Pi/10]}, MeshStyle -> Directive[AbsolutePointSize[5], Red], PlotStyle -> Blue]. – J. M.'s missing motivation Jul 24 '12 at 23:36
@MarkAdler Could you add an example of the functions you're plotting? – rm -rf Jul 24 '12 at 23:40
@J.M. Yes, I noticed wxffles' comment after I'd written it. Will fix in the next edit – rm -rf Jul 24 '12 at 23:40
@MarkAdler Are your functions smooth or at least, differentiable once? – rm -rf Jul 24 '12 at 23:42
Ah, my mistake. Your ParametricTimePlot with line segment ticks is working perfectly with my interpolating functions. Thanks! – Mark Adler Jul 24 '12 at 23:52
I was trying to get the ticks to use PlotStyle. To do that, I changed Line[...] to {OptionValue[PlotStyle],Line[...]}. That actually worked, but now I get a bunch of nastygrams about unknown options for ParametricTimePlot for the other options that I'm passing to ParametricPlot (Frame, FrameLabel, etc.). – Mark Adler Jul 25 '12 at 00:04
@MarkAdler That's because I had intended to only supply the options to ParametricPlot, not use them in any other way, so didn't define any defaults. To do what you want, replace the opts in the definition with opts : OptionsPattern[Options[ParametricPlot]] – rm -rf Jul 25 '12 at 00:07
That did it! Thanks again. – Mark Adler Jul 25 '12 at 00:09
@MarkAdler Even simpler would be just using OptionValue[opts, PlotStyle] (no need to change opts) – rm -rf Jul 25 '12 at 00:09

score 3 · Answer 2 · answered Jul 24 '12 at 23:03

One way to do it would be to find analytically the parallel line yourself, and then creating a Graphics[] with all the lines. Here is a rough working example that's specific to this one expression and scales the lines according to the differential of the function, but it outlines the gist of the idea.

Show[
Line /@ Table[
Evaluate[
     {Cos[t^2], Sin[t^2]} + 
        (0.1/2 tickpoint D[{Cos[t^2], Sin[t^2]}, t] // {#[[2]], -#[[1]]} &)
]
, {t, 0, 2.5, 0.05}, {tickpoint, {-1, 1}}] // Graphics,
ParametricPlot[{Cos[t^2], Sin[t^2]}, {t, 0, 2.5}]
]

ParametricPlot combined with ticks showing regular intervals of the parameter

score 2 · Answer 3 · answered Jul 24 '12 at 23:04

I couln't get nice little lines so I've used filled circles instead. I hope this works.

I've spaced the points out but Pi/4 on the curve in this example.

f = {Sin[#], Sin[2 #]} &
Show[
 ParametricPlot[f[u], {u, 0, 2 \[Pi]}],
 ListPlot[f /@ Range[0, 2 \[Pi], \[Pi]/4], 
  PlotStyle -> Directive[PointSize[0.02], Black]]
 ]

" Mathematica graphic "

Is there an easy way to put time ticks on a parametric plot?

3 Answers3

Linked

Related