Visualize scalar field $f(x,y,z)$ in three dimension

Question

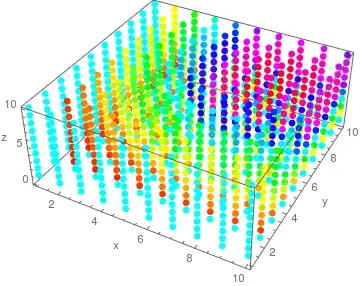
I am trying to visualize scalar field in three dimension generated from some simulations with tuples $(x, y, z, w)$ where $w=f (x, y, z)$.

Here is my first attempt

f[x_, y_, z_] := Sin[x/4]*Sin[y/4]*Sin[z/4];
xyzw = Flatten[Table[{x, y, z, f[x, y, z]}, {x, 1, 10}, {y, 1, 10}, {z, 1, 10}] //N, 2];

M = 10;
xyz = xyzw[[;; , {1, 2, 3}]];
w = ArrayReshape[xyzw[[;; , 4]], {M, M, M}];
f[x_, y_, z_] := w[[Round[x] + 1, Round[y] + 1, Round[z] + 1]];

f = ListPointPlot3D[xyz, 
  ColorFunction -> Function[{x, y, z}, Hue[f[x*M, y*M, z*M]]], 
  AxesLabel -> {"x", "y", "z"}, PlotStyle -> PointSize[Large]]

And here is the plot:

Some points are missing using this method which generates error, but the key problem is that it is hard to visualize what's scalar field in there, particular with millions of points.

Instead of using small points, is it possible to have filled regular cubes without any gaps so that the inner points is not visible when there are surface points? And then, how can I see any cross-section?

Another possibility: http://mathematica.stackexchange.com/questions/38656/how-to-plot-contours-in-the-faces-of-a-cube — Michael E2, Aug 10 '15 at 10:19

score 7 · Accepted Answer · edited Aug 09 '15 at 22:36

7

In version 10.2 there is a new suite of functions that may be helpful:

f[x_, y_, z_] := Sin[x/4]*Sin[y/4]*Sin[z/4];
xyzw = Flatten[Table[{x, y, z, f[x, y, z]}, {x, 1, 10}, {y, 1, 10}, {z, 1, 10}] // N, 2];
ListSliceContourPlot3D[xyzw, "CenterPlanes"]

edited Aug 09 '15 at 22:36

RunnyKine

33,088
3
109
176

answered Aug 09 '15 at 21:02

mfvonh

8,460
27
42

Do you know if they have non-planar "slice"? For example, a spherical shell surface? As I am working on non-straight shape. – unsym Aug 09 '15 at 21:07
That's new in 10.2, not in 10.0, it seems. – Szabolcs Aug 09 '15 at 21:09
@hwlau Well, did you look up the function in the documentation? – Szabolcs Aug 09 '15 at 21:10
ohh, i see. That's why I didn't find it. 10.2 really introduce more visualization. – unsym Aug 09 '15 at 21:10

score 5 · Answer 2 · answered Aug 09 '15 at 20:53

5

There are several options you can try:

ContourPlot3D is one way. You can use multiple transparent contours.

DensityPlot3D was introduced in version 10.2, but the same effect can be achieved manually using Image3D or Raster3D. The latter has the ClipRange option for cutting away a part (visualizing a cross-section).

answered Aug 09 '15 at 20:53

Szabolcs

234,956
30
623
1,263

The results is not quite continuous at some regime, so the contourplot is too messy. – unsym Aug 09 '15 at 20:56
Thanks, densityplot3D is interesting. I am looking for something more like http://mathematica.stackexchange.com/a/17266/7614 for irregular domain. – unsym Aug 09 '15 at 21:04

Visualize scalar field $f(x,y,z)$ in three dimension

2 Answers2

Linked