In the DiscretizeRegion documentation:
The region reg can be anything that is
ConstantRegionQandRegionEmbeddingDimensionless than or equal to 3.
With DiscretizeRegion there could be an easy way to check volume calculations.
First, I do it with a test region:
reg3D = ImplicitRegion[x - 2 < y < x - 1 && 0 < z < (x + y)/(x - y),
{{x, 0, 2}, {y, -2, 0}, {z, 0, 3}}];
{RegionEmbeddingDimension @ reg3D, ConstantRegionQ @ reg3D}
{3, True}
{Volume @ reg3D // N, Volume @ DiscretizeRegion[reg3D]}
{0.375, 0.373509}
Now my problem region:
reg3D = ImplicitRegion[x - 2 < y < x - 1 && 0 < z < Exp[(x + y)/(x - y)],
{{x, 0, 2}, {y, -2, 0}, {z, 0, 3}}];
{RegionEmbeddingDimension @ reg3D, ConstantRegionQ @ reg3D}
{3, True}
{vol = Volume @ reg3D, vol // N}
{(3 (-1 + E^2))/(4 E), 1.7628}
Volume @ DiscretizeRegion[reg3D];
DiscretizeRegion::drf: DiscretizeRegion was unable to discretize the region ImplicitRegion[<<2>>]. >>
Error; yet another method:
g = RegionPlot3D[reg3D, PlotPoints -> 100]
discreteReg = DiscretizeGraphics[g // Normal] // Quiet;
{RegionDimension @ discreteReg, RegionEmbeddingDimension @ discreteReg}
{2, 3}
I am now able to obtain the area:
Area @ discreteReg
12.5795
but not the volume, it fails once again.
<< NDSolve`FEM`
ToElementMesh @ discreteReg
MeshRegion::dgcell: The cell Polygon[{41,11121,408,403}] is degenerate. >> ToBoundaryMesh::femtemnm: A mesh could not be generated. >>
I didn't get much further! What can I do?
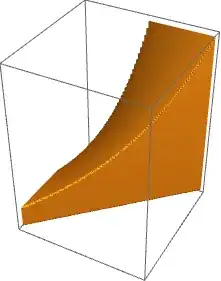

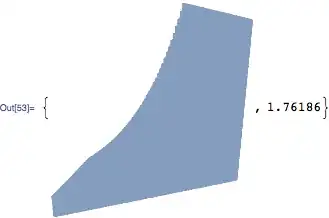
"MarchingCells"method you mention, does this have an easy solution in Mathematica? – Szabolcs Oct 04 '15 at 13:15