Is there any way to improve the result of DiscretizeRegion on this 3D ImplicitRegion?

Question

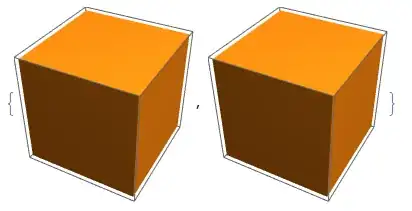
Consider two definitions of a cubic region,

a = 5;
region1 = ImplicitRegion[0 <= x <= a && 0 <= y <= a && 0 <= z <= a, {x, y, z}];
region2 = Cuboid[{0, 0, 0}, {a, a, a}];
RegionPlot3D /@ {region1, region2}

We can test whether certain points fall inside the regions

{0, 0, 0} ∈ region1
{0, 0, 0} ∈ region2
(* True *)
(* True *)

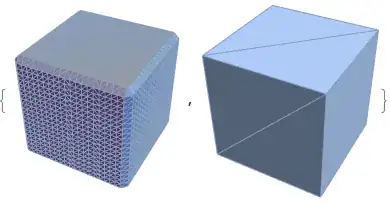
But when I try to make a DiscretizeRegion object for use in an FEM NDSolve calculation, one is clearly better than the other:

{region1dis, region2dis} = DiscretizeRegion /@ {region1, region2}

This is clear visually as well as in region tests,

# ∈ region1dis & /@ {{0, 0, 0}, {.04, .04, .04}, {.4, .4, .4}}
# ∈ region2dis & /@ {{0, 0, 0}, {.04, .04, .04}, {.4, .4, .4}}
(* {False, False, True} *)
(* {True, True, True} *)

I can't find an option for DiscretizeRegion that fixes this. Not AccuracyGoal or PrecisionGoal or MaxCellMeasure, or any of the Methods listed in this post, this post, or this post. If this is a duplicate of one of those, my apologies

Answer 1

This is a tangential answer to your question, but perhaps it may be of interest nonetheless, in the spirit of providing an alternative approach.

In the case of a cubic region you may be interested in using the bounding box option to DiscretizeRegion, rather than trying to coax it to include all the edges (which I was not yet able to do either).

For instance:

region3dis = DiscretizeRegion[
   FullRegion[3], {{0, a}, {0, a}, {0, a}},
   MaxCellMeasure -> 20
 ]

# ∈ region3dis & /@ {{0, 0, 0}, {.04, .04, .04}, {.4, .4, .4}}
(* Out: {True, True, True} *)

Incidentally, this works well with the FEM element mesh generators as well:

Needs["NDSolve`FEM`"]
ToElementMesh[FullRegion[3], {{0, 5}, {0, 5}, {0, 5}}, MaxCellMeasure -> 20]

(* Out: ElementMesh[{{0., 5.}, {0., 5.}, {0., 5.}}, {HexahedronElement["<" 8 ">"]}] *)

%["Wireframe"]