Solution
Following @MichaelSeifert's advice, here is a working solution.
First define a compact expression for a Gaussian
g[x_, xo_, σ_, a_] := a Exp[-((x - xo)^2/(2 σ^2))] /(σ Sqrt[2 π])
To get
g[x, xo, σ, Ao]
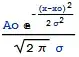
Creates a list of variables for the $k^{\text{th}}$ term.
kvar[k_Integer] :=
ToExpression@
Map[StringJoin[#, ToString[k]] &, {"x", "σ", "a"}]
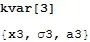
Generate a model equation to fit $n$ Gaussians using Sequence to place the output of kvar as arguments for g
gmodel[n_Integer] := Sum[
g[x, Sequence @@ kvar[i]]
, {i, 1, n}
]
Generate a list of parameters for the $n$ Gaussian model.
gpars[n_Integer] := Flatten@Array[kvar, n]
When evaluated these functions look like this:
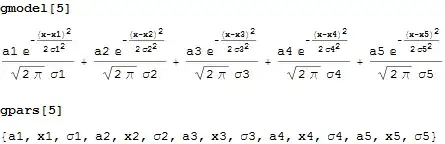
Find fit with minimal Akaike Information Criterion ( AIC ) by calculating a series of fits with 1, 2, ...maxn Gaussian, and selecting the fit with the smallest "AIC" as defined in the NonlinearModelFit documentation.
fitg[data_, maxn_Integer] := MinimalBy[
Table[
{#, #["AIC"]}& @ NonlinearModelFit[data, gmodel[n], gpars[n], x]
, {n, maxn}
], Last][[1, 1]]
Usage: fitg[data, maxn] where maxn is the maximum allowed number of Gaussians.
Possibly fitg[data, Length[data]]
Test
Example of data
dat = Uncompress@Import["http://pastebin.com/raw.php?i=VHZ7XJAi"]
Find fit with up to 6 Gaussians and plot
Show[
ListPlot[dat, PlotStyle -> Red],
Plot[Evaluate[Normal[fitg[dat, 6]]], {x, -1, 2}]
]

fitg[dat, 6]["ParameterTable"]

In this case, only three Gaussians were necessary.

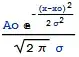
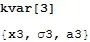
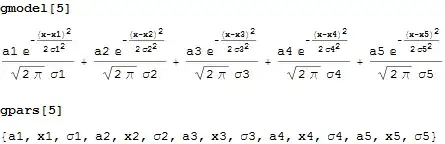


FindFormulamay well be able to do this in some future iteration, depending on how Wolfram develops it. As of now (v10.2), it appears to be limited to a small number of target functions – Michael Seifert Sep 07 '15 at 15:56