How to make Which not connect its parts?

Question

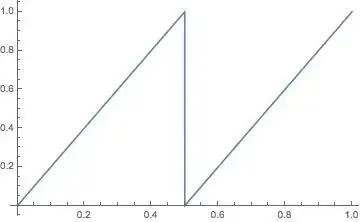
I've noticed that when "Mod" and "Which" are used to the same effect, they plot to slightly different results. Take the following example:

f[x_] = 2 x;
fmod[x_] = Mod[f[x], 1];
Plot[fmod[x], {x, 0, 1}]
fwhich[x_] = Which[x < 1/2, f[x], x > 1/2, f[x] - 1];
Plot[fwhich[x], {x, 0, 1}]

The output graphs are:

How can I graph Which without getting that connecting line?

I would suggest that you use a Piecewise function definition in your case, rather than Which: fpiece[x_] = Piecewise[{{f[x], x < 1/2}, {f[x] - 1, x > 1/2}}];. — MarcoB, Sep 10 '15 at 15:49
fmod[1/2] evaluates to 0. fwhich[1/2] is undefined. This may be related to the result you are seeing. — Jack LaVigne, Sep 10 '15 at 23:29
possible duplicate of Plotting jump function without vertical lines — Oleksandr R., Sep 11 '15 at 02:03

score 5 · Accepted Answer · edited Apr 13 '17 at 12:55

5

As MarcoB already pointed out in the comments, Piecewise is probably the better alternative.

Additionally, we already have a related question with good answers where you can steal ideas from:

f[x_] = 2 x;
fmod[x_] = Mod[f[x], 1];
fwhich[x_] = Which[x < 1/2, f[x], x > 1/2, f[x] - 1];
Plot[fwhich[x], {x, 0, 1}, Exclusions -> {1/2}]

Mathematica graphics

edited Apr 13 '17 at 12:55

Community

answered Sep 10 '15 at 15:57

halirutan

1 Answers1