I have this code:
S = (Sqrt[2]/2)*{{1 + Conjugate[δ], 0}, {0,1 - Conjugate[δ]}}(** Suppose a+b=1 and δ=((a-b)/(a+b))\[Conjugate] **)
k = (1/Sqrt[2])*{{S[[1, 1]] + S[[2, 2]]}, {S[[1, 1]] - S[[2, 2]]}, {2 S[[1, 2]]}} // Simplify
Subscript[T, 0] = Dot[k, ConjugateTranspose[k]]
Subscript[T, 0] // MatrixForm
Subscript[T, 0] // TraditionalForm
$$\left( \begin{array}{ccc} 1 & \delta & 0 \\ \delta ^* & \delta \delta ^* & 0 \\ 0 & 0 & 0 \\ \end{array} \right)$$
As you see at the end the product of $\delta$ and $\delta^*$ is not printed as $|\delta|^2$ but as $\delta\delta^*$
Someone told me in one of my questions that this is because:
It seems that you did not instruct Mma that δ∗ is a conjugated value of δ. Using simply a conjugate symbol is not enough. You should use Conjugate[δ] instead and then apply ComplexExpand
so far I have tried several ways like
Using the UpsetDelayed operator in the begining of code as:
δ\[Conjugate] ^:= Conjugate[δ]
or using:
ComplexExpand[Subscript[T,0], δ, TargetFunctions -> {Abs, Conjugate}]
But I couldn't change any thing?!
Following the the first answer posted to the question I wrote:
FullSimplify[Subscript[T, 0]] // TraditionalForm
$$\left(
\begin{array}{ccc}
1 & \delta & 0 \\
\delta ^* & \left| \delta \right| ^2 & 0 \\
0 & 0 & 0 \\
\end{array}
\right)$$
But when I continue the code and apply the same trick on another matrix, the trick doesn't work!
R[ψ_] := {{1, 0, 0}, {0, Cos[2 ψ], Sin[2 ψ]}, {0, -Sin[2 ψ], Cos[2 ψ]}}
T[ψ_] := Dot[R[ψ], Subscript[T, 0], Transpose[R[ψ]]]
FullSimplify[T[ψ]] // TraditionalForm
$$\left( \begin{array}{ccc} 1 & \delta (\cos (2 \psi )) & -\delta (\sin (2 \psi )) \\ \delta ^* (\cos (2 \psi )) & \delta \delta ^* \left(\cos ^2 (2 \psi )\right) & -\frac{1}{2} \delta \delta ^* (\sin (4 \psi )) \\ -\delta ^* (\sin (2 \psi )) & -\frac{1}{2} \delta \delta ^* (\sin (4 \psi )) & \delta \delta ^* \left(\sin ^2 (2 \psi )\right) \\ \end{array} \right)$$
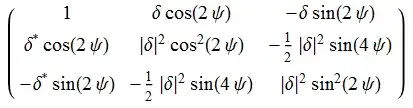
d d*toAbs[d^2]orAbs[d]^2, however there is a sort of explanation to this. IIRC, MMA judges the complexity of an expression by itsLeafCount. Bothd d*andAbs[d]^2(as well asAbs[d^2]) have aLeafCountof4, so I guess, it feels no need to "simplify". I completely agree, that it is frustrating. – LLlAMnYP Sep 18 '15 at 07:01