8

Bug introduced in 8.0 or earlier and persisting through 13.2 or later. Fixed in 13.3.1 on Windows 10

I have the following mapping on the complex plane: $$ z \mapsto \tau \mu z-1, $$ where $\mu$ is complex, $\tau$ is real number. I want to draw the image of left unit semidisk and play with $\tau$.

μ = 0.16255558520216132` + 0.1849493244071408` I;

pic[τ_] := Block[{d, ds},
   d = Disk[{0, 0}, 1, {π/2, 3 π/2}];
   ds =
    Fold[GeometricTransformation, d,
       {RotationTransform[Arg@#, {0, 0}],
        ScalingTransform[τ Abs@# {1, 1}],
        TranslationTransform[{-1, 0}]
        }] & @ μ;
   Graphics@{Gray, d, Red, Opacity[.5], ds}
   ];


Manipulate[
 Dynamic@Show[pic[τ], Frame -> True, Axes -> True, 
   AxesOrigin -> {0, 0}, PlotRange -> zz {{-100, 100}, {-100, 100}},
   ImageSize -> 400
   ],
 {τ, 0.01, 1000, 0.01},
 {zz, 0.01, 10, 0.01}
 ]

Here zz is introduced to control zooming. The problem is that I get different (wrong) images for different zooms. It is clearly seen for big $\tau$'s.

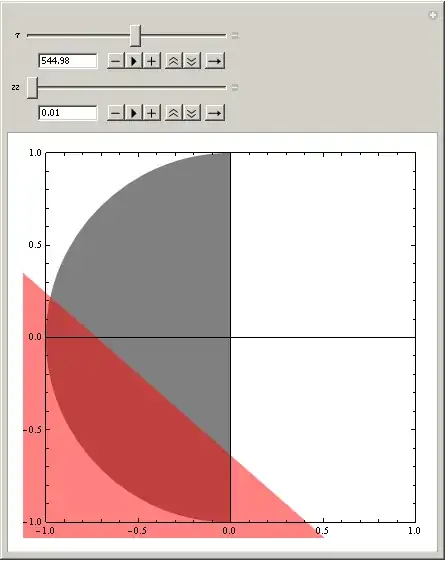
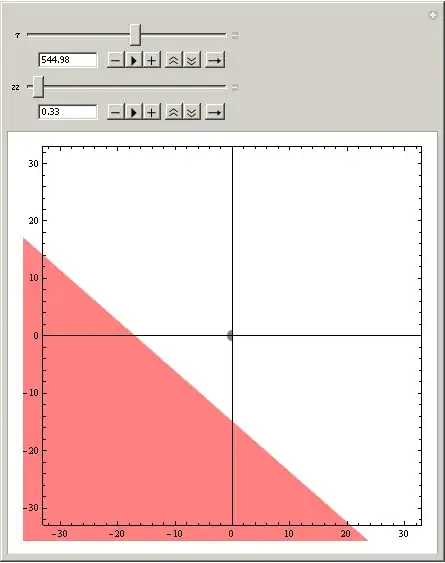
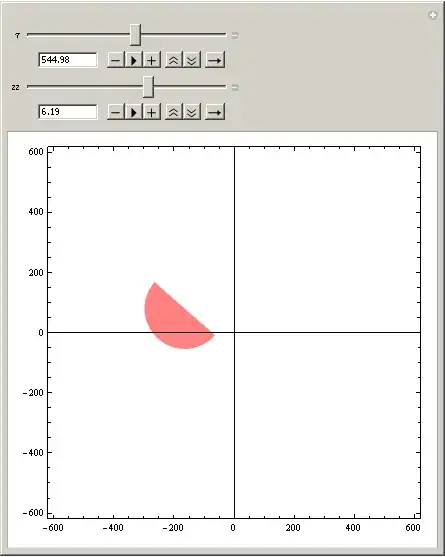
enter image description hereenter image description hereenter image description here

It looks very like a bug, but I can not rule out that I'm making some silly mistake (Mathematica 8.0.4). So, what is the problem here and what is the best way of doing the job (I have several mappings for different $\mu$ actually)?

user64494
  • 26,149
  • 4
  • 27
  • 56
faleichik
  • 12,651
  • 8
  • 43
  • 62
  • 1
    I'd have implemented pic[] this way: pic[τ_] := Block[{d, ds}, d = Disk[{0, 0}, 1, {π/2, 3 π/2}]; ds = GeometricTransformation[d, Composition[TranslationTransform[{-1, 0}], ScalingTransform[τ Abs[μ] {1, 1}], RotationTransform[Arg[μ], {0, 0}]]]; Graphics @ {Gray, d, Red, Opacity[.5], ds}] – J. M.'s missing motivation Aug 17 '12 at 17:24
  • 3
    Here's another way to visualize your transformation of a disk: ParametricPlot[Through[{Re, Im}[τ μ r Exp[I θ] - 1]], {r, 0, 1}, {θ, π/2, 3 π/2}]] – J. M.'s missing motivation Aug 17 '12 at 17:38
  • @J.M. thank you very much! Unfortunately Composition produces the same erroneous result. ParametricPlot is a viable alternative. Still the problem with composite GeometricTransformations remains. – faleichik Aug 17 '12 at 20:18
  • 2
    Minimal example of the problem: Evaluate Graphics@GeometricTransformation[Disk[],Composition[ScalingTransform[{800,800}],RotationTransform[0.1,{0,0}]]] and resize the graphic with the mouse. – Simon Woods Aug 17 '12 at 21:41
  • "Unfortunately Composition produces the same erroneous result." - I suppose so; all I did was to shorten the code you used for producing the transformed disk ds. – J. M.'s missing motivation Aug 18 '12 at 00:41
  • @SimonWoods +1. And for Disk[{0, 0}, 1, {0, a}], if non-empty EdgeForm is used, if a is close enough to 2*Pi, the edge and the filled body "jump" together, if a is far away from 2*Pi, say 3*Pi/2, the edge alone seems working right. – Silvia Aug 18 '12 at 17:35
  • 1
    You can apply the transformations beforehand to the key-coordinates of the disk, which transforms Disk[{0, 0}, 1, {α, β}] to Disk[{-1, 0}, τ Abs[μ], {α, β} + Arg[μ]]. This explicit form will work fine with Graphics. – Silvia Aug 18 '12 at 17:57
  • Fixed in 13.3.1 on Windows 10. – user64494 Dec 05 '23 at 06:37

1 Answers1

4

This is surely a bug. The misbehavior certainly persists through V10.2. In fact, the two images below are of the same computation. The only difference is where they appear on the screen (as I scrolled the notebook, the transformed red disk jumped around).

μ = 0.16255558520216132` + 0.1849493244071408` I;

pic[τ_] := Block[{d, ds, arc},
   d = Disk[{0, 0}, 1, {π/2, 3 π/2}];
   ds = GeometricTransformation[d, 
       TranslationTransform[{-1, 0}] . 
        ScalingTransform[τ Abs@# {1, 1}] .
        RotationTransform[Arg@#, {0, 0}]] &@ μ;
   Graphics@ {Gray, d, Red, Opacity[.5], ds}];

Manipulate[
 Dynamic@Show[pic[τ], Frame -> True, Axes -> True, 
   AxesOrigin -> {0, 0}, PlotRange -> 100 zz , 
   ImageSize -> 222],
 {τ, 0.01, 1000, 0.01}, {zz, 0.01, 10, 0.01}]

As others have observed, PlotRange and ImageSize can affect what is displayed.

Note that the graphics are sent to the front end with the disk inside GeometricTransformationBox (one with my code, three nested ones with the OP's code). They appear to be correct, so the issue is with the front end (or possibly the GPU, I suppose). The workarounds by Silvia and J. M. avoid the use of GeometricTransformationBox. This sort of misbehavior has been noted since, e.g. Weird behaviour when using Scale, Rotate in Graphics.

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747