Lloyd relaxation on VoronoiMesh

Question

How can we apply Lloyd's relaxation algorithm to a VoronoiMesh?

Thanks.

UPDATE

Thanks a lot KennyColnago for your answer. Based on Simon Woods suggestion of using PropertyValue[{vmesh, 2}, MeshCellCentroid], I think this code can be simplified a bit, e.g.

VoronoiAdaptive2[p_, iter_] := Block[{vmesh = VoronoiMesh[p]},
Do[
vmesh = VoronoiMesh[PropertyValue[{vmesh, 2}, MeshCellCentroid]],
{i, iter}];
vmesh];

Now I have a question about the algorithm itself: According to Wikipedia,

Each time a relaxation step is performed, the points are left in a slightly more even distribution: closely spaced points move farther apart, and widely spaced points move closer together.

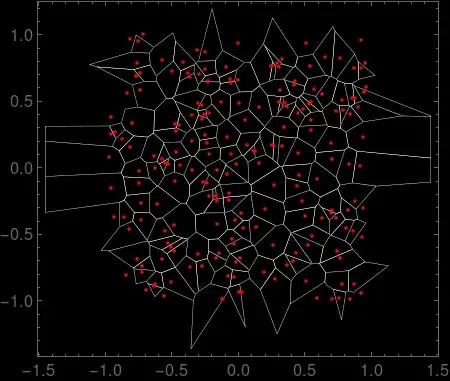
But using a large number of iterations with the above code results in a mesh with a concentration of very small cells in the center and large cells on the boundary (omitting the line of KennyColnago's code that excludes cells beyond a certain radius).

For example, with 200 points and the same random seed as KennyColnago and 200 iterations, the following mesh is produced:

SeedRandom[1729];
VoronoiAdaptive2[RandomReal[{-1, 1}, {200, 2}], 200]

200 iters

Going up to 1200 iterations produces a visually identical image. Is this the expected output? I was hoping to see something more like on this website

It would help potential answerers if you included some code to generate a VoronoiMesh to work with, and any progress you have made in solving the problem yourself. Did you try implementing the description of the algorithm in the linked Wikipedia article? — Simon Woods, Oct 03 '15 at 17:19
For a neat application (v10) of adaptive Voronoi meshes to images, see the Help page for VoronoiMesh > Applications > Image Processing. With iteration, the cells become nearly circular, and their sizes adapt locally to the image structure. — KennyColnago, Dec 25 '15 at 01:35
You might be interested in section 3 of my post on the Wolfram Community. — Silvia, Mar 09 '16 at 05:12

J. M.'s missing motivation · Answer 1 · 2017-08-03T14:43:52.693

Here's my take on Lloyd's algorithm. The code I present here should not be too hard to encapsulate into a routine; I have only elected to present it in this way so that I can animate the progress of the relaxation method:

BlockRandom[SeedRandom[42, Method -> "Legacy"]; (* for reproducibility *)
            pts = RandomReal[{-1, 1}, {50, 2}]];

pl = With[{maxit = 50, (* maximum iterations *)
           tol = 0.005 (* distance tolerance *)}, 
          FixedPointList[Function[pts, Block[{cells},
                         cells = MeshPrimitives[VoronoiMesh[pts,
                                                {{-1, 1}, {-1, 1}}], "Faces"];
                         RegionCentroid /@ cells[[SparseArray[
                         Outer[#2 @ #1 &, pts, RegionMember /@ cells, 1],
                         Automatic, False]["NonzeroPositions"][[All, 2]]]]]],
                         pts, maxit, 
                         SameTest -> (Max[MapThread[EuclideanDistance,
                                                    {#1, #2}]] < tol &)]];

MapThread[Show, {VoronoiMesh /@ Rest[pl], 
                 MapThread[Graphics[{AbsolutePointSize[3], Line[{##}],
                                    {Black, Point[#1]}, {Red, Point[#2]}}] &,
                           #] & /@ Partition[pl, 2, 1]}] // ListAnimate

Lloyd relaxation

Note: I elected not to use PropertyValue[{(* mesh *), 2}, MeshCellCentroid], since the centroids are not returned in the same order as the points that generated their corresponding cells, thus necessitating a complicated termination criterion.

In this answer, ilian shows an undocumented function that can be used to simplify the implementation of Lloyd's algorithm. Here's how it goes:

pl = With[{maxit = 50, (* maximum iterations *)
           tol = 0.005 (* distance tolerance *)}, 
          FixedPointList[Function[pts, Block[{cells, ci, vm},
                         vm = VoronoiMesh[pts, {{-1, 1}, {-1, 1}}];
                         cells = MeshPrimitives[vm, "Faces"]; 
                         ci = Region`Mesh`MeshMemberCellIndex[vm];
                         RegionCentroid /@ cells[[ci[pts][[All, -1]]]]]], pts, maxit, 
                         SameTest -> (Max[MapThread[EuclideanDistance,
                                                    {#1, #2}]] < tol &)]];

This is nice. Thanks for pointing me to this. I still think it's crazy there's no easy way to get corresponding cells for the sites. — RunnyKine, Mar 10 '16 at 19:35
It annoys me a lot that I had to complicate my implementation here because of this scrambling. Maybe if enough of us complain… — J. M.'s missing motivation, Mar 10 '16 at 19:43

score 8 · Accepted Answer · answered Oct 04 '15 at 11:02

To address the update to the question, you can use the second argument of VoronoiMesh to set a rectangular boundary which will let the algorithm converge to a uniform spacing. It looks like the linked animation is also inserting additional points at the centre, or perhaps it starts with a high density of points near the centre of the mesh. Here is something similar - I keep inserting a point at {0,0} until there are 200 points:

vmesh = VoronoiMesh[RandomReal[{-1, 1}, {20, 2}]];
Dynamic[
 pts = PropertyValue[{vmesh, 2}, MeshCellCentroid];
 If[Length@pts < 200, AppendTo[pts, {0, 0}]];
 vmesh = VoronoiMesh[pts, {{-1, 1}, {-1, 1}}]]

score 6 · Answer 3 · answered Oct 03 '15 at 18:22

The following imperfect code is what I play with. Given an input set of points p, run VoronoiMesh iter times, each time replacing the points with the centroids of the cells.

VoronoiAdaptive[p_, iter_] :=
   Block[{points = p, vmesh, coord, poly, centroids, 
          error = ConstantArray[0, iter]},
         vmesh = VoronoiMesh[points];
         coord = MeshCoordinates[vmesh];
         poly = MeshCells[vmesh, 2];
         centroids = Map[Mean[coord[[#[[1]]]]] &, poly];
         Do[
            points = centroids;
            vmesh = VoronoiMesh[points];
            coord = MeshCoordinates[vmesh];
            poly = MeshCells[vmesh, 2];
            centroids = Map[Mean[coord[[#[[1]]]]] &, poly];
            error[[i]] = Mean[Abs[Flatten[points - centroids]]],
            {i, 1, iter}];
         Print[error];
         {coord, poly}
   ]

Here is a plot of the original mesh for 200 random points. Cells with vertices outside an arbitrary radius of 1.5 are removed.

Block[{p, coord, poly, iter = 0},
   SeedRandom[1729];
   p = RandomReal[{-1, 1}, {20, 2}];
   {coord, poly} = VoronoiAdaptive[p, iter];
   poly = DeleteCases[poly, _?(Max[Map[Norm, coord[[#[[1]]]]]] > 1.5 &)];
   Graphics[{PointSize[0.02],
      EdgeForm[{Thickness[0.001], White}],
      GraphicsComplex[coord, poly],
      Red, Point[p],
      Frame -> True, Background -> Black]
]

Setting iter=10 gives the following.

You could use PropertyValue[{vmesh, 2}, MeshCellCentroid] to get the centroids — Simon Woods, Oct 03 '15 at 18:33
Thanks a lot, @KennyColnago. I'm wondering though why using a large number of iterations doesn't produce a very uniform mesh like in the animation here. — nasosev, Oct 04 '15 at 00:20

Lloyd relaxation on VoronoiMesh

3 Answers3

Linked