Site - Cell Correspondence in Voronoi Diagram obtained via VoronoiMesh

Question

Consider the following:

pts = RandomReal[4, {10, 2}];
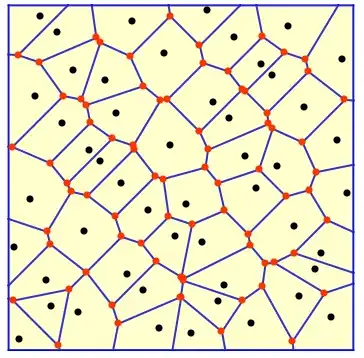
vor = VoronoiMesh[pts, {{0, 4}, {0, 4}}];

Graphics[{GraphicsComplex[
   MeshCoordinates[vor], {Thick, Blue, MeshCells[vor, 1], 
    PointSize[0.02], Red, MeshCells[vor, 0], Opacity[0.2], Yellow, 
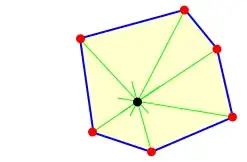
    MeshCells[vor, 2]}], PointSize[0.02], Point[pts[[1]]], Green, 
  MeshPrimitives[vor, 2][[1]]}]

Looking at the above, we see that the Voronoi sites (points that generate the Voronoi diagram) do not correspond to the Voronoi cells (in the order) generated by VoronoiMesh. Since VoronoiMesh discards the points used in generating the diagram, there's no obvious way I can see to align the Voronoi sites with their corresponding cells. This feels like an oversight to me, since one will have to do some complex post-processing to obtain such correspondence.

My question is: is there an easy way to obtain a site - cell alignment of the Voronoi diagram obtained via VoronoiMesh other than using e.g. RegionMember which seems like an unnecessary overkill when this information should be available in the Mesh object. So e.g. with the points above, an output of the form shown below is desirable:

Transpose[{pts, MeshCells[vor, 2]}]

{{{3.15429516, 1.68154241}, Polygon[{20, 11, 6, 15}]}, 
 {{0.925806386, 3.57266721}, Polygon[{12, 3, 1, 13}]}, 
 {{2.12535296, 3.88158116}, Polygon[{14, 5, 8, 18}]},
 {{3.52419343, 0.689832144}, Polygon[{18, 8, 7, 17}]},
 {{0.590442758, 1.53821808}, Polygon[{10, 4, 9, 6, 11}]},
 {{2.70632597, 3.81614775}, Polygon[{19, 13, 1, 5, 14}]},
 {{2.23994147, 1.5141697}, Polygon[{15, 6, 9, 2, 16}]},
 {{3.68657472, 2.93505855}, Polygon[{16, 2, 3, 12, 21}]},
 {{0.12127097, 2.63380289}, Polygon[{17, 7, 4, 10, 22}]},
 {{2.21266451, 2.69765978}, Polygon[{1, 3, 2, 9, 4, 7, 8, 5}]}}

Answer 1

There is also a currently undocumented internal function that may be useful.

Region`Mesh`MeshMemberCellIndex[mr] generates a function which can be applied to list of points, giving for each pt the index of the (first encountered) highest-dimensional cell of mr containing pt. For example,

Region`Mesh`MeshMemberCellIndex[vor][pts]

(* {{2, 2}, {2, 4}, {2, 5}, {2, 3}, {2, 9}, {2, 1}, {2, 10}, {2, 7}, {2, 8}, {2, 6}} *)

pt = pts[[1]]; 
Graphics[{GraphicsComplex[MeshCoordinates[vor], 
   {Thick, Blue, MeshCells[vor, 1], 
    PointSize[0.02], Red, MeshCells[vor, 0], 
    Opacity[0.2], Yellow, MeshCells[vor, 2]}], 
    PointSize[0.02], Magenta, Point[pt], 
    Opacity[0.2], Green, MeshPrimitives[vor, Region`Mesh`MeshMemberCellIndex[vor][pt]]}]

Answer 2

Of course it's not good that Mathematica forget initial points for Voronoi mesh. May be it is a bug. However one can easily recover all generating points directly from the mesh. It's interesting from theoretical point of view.

Let's consider one point of the Voronoi mesh

There are three pairs of equal angles $\alpha,\beta,\gamma$ around this point. Therefore $\alpha+\beta+\gamma=\pi$. Hence we know $$ \gamma = \pi-(\alpha+\beta) $$ where $\alpha+\beta$ is an angle between known vectors ${\bf r}_1$ and ${\bf r}_2$. Then we can rotate ${\bf r}_3$ by angle $\gamma$ (to the left or the right) and obtain a ray to one of the generating points. Intersection of rays from different points will give the position of a generating point.

Here it is my realization of this method.

SeedRandom[0, Method -> {"MKL", Method -> {"Sobol", "Dimension" -> 2}}];
(* Voronoi cells looks better with sobol low-discrepancy random sequence *) 
pts = RandomReal[4, {50, 2}];
boundary = {{0, 4}, {0, 4}};
vor = VoronoiMesh[pts, boundary];

q = MeshCoordinates[vor];
conn = # + #\[Transpose] &@
    SparseArray[# -> ConstantArray[1, Length@#], {1, 1} Max@#] &[# & @@@MeshCells[vor, 1]];
in = Flatten@Position[q, {x_, y_} /; 
     boundary[[1, 1]] < x < boundary[[1, 2]] && boundary[[2, 1]] < y < boundary[[2, 2]]];
(* points inside boundaries *)

g = Graphics@{GraphicsComplex[
MeshCoordinates@vor, {Thick, Blue, MeshCells[vor, 1], 
 PointSize@0.02, Red, MeshCells[vor, 0][[in]], Opacity@0.2, 
 Yellow, MeshCells[vor, 2]}], PointSize@0.02, Point@pts}

cells = MeshCells[vor, 2];
δ = {{1, 0}, {0, 1}};
e = {{0, -1}, {1, 0}};
c = e\[TensorProduct]δ - δ\[TensorProduct]e;
p1 = If[Length@# < 2, {}, LeastSquares@##] & @@ 
 Transpose@With[{pin = # ⋂ in, p = #}, 
   With[{a = c.(#4 - #).(#3 - #).(#2 - #)}, {a, a.#}] & @@@ 
    MapIndexed[q[[Join[pin[[#2]], # ⋂ p, #~Complement~p]]] &, 
     conn[[pin]]@"AdjacencyLists"]] & @@@ cells;
Show@{g, Graphics@{Orange, PointSize@0.02, Point@DeleteCases[p1, {}]}}

Inside the second With # is one of the not-boundary points in the Voronoi mesh. #2 and #3 is two neigbour points in the same polygon. #4 is the neigbour point in another polygon. The matrix c make proper rotation to obtain a vector a, which is perpendicular to a ray.

Unfortunately there some generating points near edge, which we can not find by ray intersection (there are less then two rays). I mark these remain points by {} and denote by rem. We will find them by reflection of calculated points (denoted by calc).

rem = Flatten@Position[p1, {}];
calc = Complement[Range@Length@cells, rem];
edges = Partition[#, 2, 1, 1]~Join~Partition[Reverse@#, 2, 1, 1] & @@@ cells[[calc]];
p1[[rem]] = Mean /@ DeleteCases[
   If[p1[[calc]][[#]] != {}, 
       ReflectionTransform[Cross[Subtract @@ q[[edges[[##]]]]], 
         q[[edges[[##, 1]]]]]@p1[[calc]][[#]], {}] & @@@ 
   DeleteCases[Join @@ Position[edges, #] & /@ Partition[#, 2, 1, 1], {}] & @@@
  MeshCells[vor, 2][[Flatten@Position[p1, {}]]], {}];
Max@Abs[Sort@pts - Sort@p1]

We recover all points with high precision! Of course, the order of points is the same as in MeshCells.

3.9968*10^-15

Answer 3

While I await other answers, here is the RegionMember approach I mentioned:

cellSite[p_, reg_] := With[{rm = RegionMember[reg]}, {Point@Flatten@Pick[p, rm[p]], reg}]

Then:

cs = cellSite[pts, #] & /@ MeshPrimitives[vor, 2];

Visualize:

GraphicsGrid[
 Partition[Graphics[{GraphicsComplex[MeshCoordinates[vor], {Thick, Blue, MeshCells[vor, 1], 
 PointSize[0.02], Red, MeshCells[vor, 0], Opacity[0.2], Yellow, MeshCells[vor, 2]}], 
 PointSize[0.02], #1, Opacity[0.2], Green, #2, Red}] & @@@ cs, 5], ImageSize -> 700]

Answer 4

c = PropertyValue[{vor, 2}, MeshCellCentroid];
cents = Join @@ (Nearest @ pts /@c);
cs2 = Thread[{Point/@cents,MeshPrimitives[vor, 2]}];
cs2 == cs
(* True *)

Grid[Partition[Graphics[{GraphicsComplex[MeshCoordinates[vor],
                            {Thick, Blue, MeshCells[vor, 1],
                            PointSize[0.02], Red, MeshCells[vor, 0], Opacity[0.2], 
                            Yellow, MeshCells[vor, 2]}],       
                         PointSize[0.02], #, Opacity[0.2],Green, #2, Red}] &@@@ cs2,5]]

Answer 5

Another simple solution in my this post but very slow

pts = RandomReal[4, {10, 2}];
vor = VoronoiMesh[pts, {{0, 4}, {0, 4}}];
poly = MeshPrimitives[vor, 2];

AbsoluteTiming[
 youWant = 
  List @@@ EdgeList@Quiet[RelationGraph[RegionMember, poly, pts]]; 
 RegionMember @@@ youWant]

{0.414993,{True,True,True,True,True,True,True,True,True,True}}

But I don't know why I get some error informations when I don't use Quiet.

---

Another more fast method can do this

youWant = Quiet[Gather[Join[pts, poly], # || RegionMember[#2, #] &]]