I want to calculate the integral:
$$A_n=\int_0^{2\pi}\cos^{2n}(\theta-\theta_0)\mathrm d\theta$$
assuming that we are familiar with the relation:
$$\cos^{2n}x=\frac1{2^{2n}}\binom{2n}{n}+\frac1{2^{2n-1}}\sum_{k=0}^{n-1}\binom{2n}{k}\cos2(n-k)x$$
The answer should be:
$$A_n=\frac{\pi}{2^{2n-1}}\binom{2n}{n}$$
The code that I've used is the following:
$Assumptions = n ∈ Integers;
substitute =
{(Cos[x_])^(2 n) ->
1/2^(2 n) Binomial[2 n, n] + 1/2^(2 n - 1) *
Sum[Binomial[2 n, k] Cos[2 (n - k) x], {k, 0, n - 1}]};
But I see that substitution is not done correctly:
Cos[θ - μ]^(2 n) /. substitute
$2^{-2 n} \binom{2 n}{n}+2^{-2 n} e^{-2 i n (\theta -\mu )} \left(-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{-2 i (\theta -\mu )}\right)-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{2 i (\theta -\mu )}\right)+e^{4 i n (\theta -\mu )} \left(1+e^{-2 i (\theta -\mu )}\right)^{2 n}+\left(1+e^{2 i (\theta -\mu )}\right)^{2 n}\right)$
And the integral is calculated as:
A = Integrate[Cos[θ - μ]^(2 n) /. substitute, {θ, 0, 2 Pi}, Assumptions -> 0 <= μ <= 2 Pi]
$\text{Integrate}\left[2^{-2 n} \binom{2 n}{n}+2^{-2 n} e^{-2 i n (\theta -\mu )} \left(-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{-2 i (\theta -\mu )}\right)-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{2 i (\theta -\mu )}\right)+e^{4 i n (\theta -\mu )} \left(1+e^{-2 i (\theta -\mu )}\right)^{2 n}+\left(1+e^{2 i (\theta -\mu )}\right)^{2 n}\right),\{\theta ,0,2 \pi \},\text{Assumptions}\to 0\leq \mu \leq 2 \pi \right]$
Is there any way to force mathematica calculate the explicit solution of the integral?
Edit: I wonder why I get the result:
Integrate[(Cos[t - t0])^(2 n), {t, 0, 2 Pi},
Assumptions ->
n ∈ Integers && t0 ∈ Reals &&
0 <= t0 < 2 Pi] // AbsoluteTiming
(*
{133.223,
Integrate[Cos[t - t0]^(2 n), {t, 0, 2 \[Pi]},
Assumptions ->
n ∈ Integers && t0 ∈ Reals && 0 <= t0 < 2 \[Pi]]}
*)
After considering all the information I gained from following links:
Singular integral mathematica
Correct way to integrate a certain function
Bug in mathematica analytic integration?
Suspected bug in Integrate
I also wrote the following code:
r := RandomReal[{0, 2 Pi}]
Integrate[(Cos[t - t0])^(2 n) /. t0 -> r, {t, 0, 2 Pi},
Assumptions -> n ∈ Integers] // AbsoluteTiming
(*
{6.18195,
1/((0.5 + 1. n) Gamma[
1. + n]) ((1.77245 + 1.77245 E^((0. + 6.28319 I) n)) Gamma[
1.5 + n] +
Gamma[1. +
n] (-0.421391 E^(-0.342092 n)
Hypergeometric2F1[0.5, 0.5 + 1. n, 1.5 + 1. n, 0.710283] +
0.421391 E^(-0.342092 n)
Hypergeometric2F1[0.5, 0.5 + 1. n, 1.5 + 1. n, 0.710283]))}
*)
seems that I can never reach the solution
(*
{19.1049,
ConditionalExpression[((1 + (-1)^(2 n)) Sqrt[π] Gamma[1/2 + n])/Gamma[1 + n],
Cos[x0] >= 0 && 2 π < x0 <= (5 π)/2]}
*)
expressed by @MichaelE2
Edit: I finally wrote the following code and I get the result except that I don't understand why is Global needed in my answer:
int = Simplify[(Cos[t - t0])^(2 n) Dt[t] /. t -> t0 + x //
TrigExpand] /. {Dt[t0] -> 0, Dt[x] -> 1}
(*
Cos[x]^(2 n)
*)
Integrate[int, {x, -t0, 2 Pi - t0},
Assumptions ->
n ∈ Integers && n > 0 && t0 ∈ Reals &&
0 <= t0 < 2 Pi]
(*
ConditionalExpression[((1 + (-1)^(2 Global`n)) Sqrt[\[Pi]]
Gamma[1/2 + Global`n])/Gamma[1 + Global`n],
Global`t0 > 0 && 2 Global`t0 <= \[Pi]]
*)
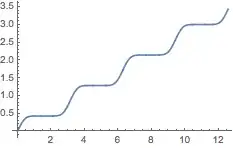


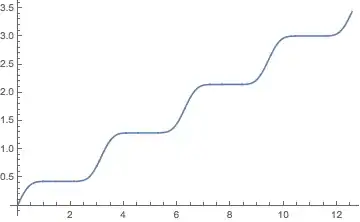
The antiderivative is easily determined by Mathematica but it is not continuous in the interval of integration but there are jumps which have to be taken into account when using the fundamental theorem of calculus.
See e.g. my answer to http://mathematica.stackexchange.com/questions/92044/singular-integral-mathematica
– Dr. Wolfgang Hintze Oct 13 '15 at 16:22Integrate). User variables normally are created in theGlobal`context, but I don't know why it shows up explicitly printed in the output. – Michael E2 Oct 15 '15 at 11:56Cos[x]^(2 n)with a symbolic parameternis not known to (or not computed by) Mathematica. Consideri = Integrate[Cos[x]^(2 n), x]; Block[{n = 1}, Plot[i, {x, 0, 4 Pi}]]. The "antiderivative"ihas a periodic discontinuity. Consider alsoBlock[{n = 1}, Evaluate@Integrate[Cos[x]^(2 n), x]]andBlock[{n = 1}, Integrate[Cos[x]^(2 n), x]]. For explicit numericn(the 2nd example), M can compute a general antiderivative. -- The only relevance is that it shows the difficulty underlying your integral. – Michael E2 Oct 15 '15 at 12:12Global'isn't printed in the output anymore – Sepideh Abadpour Oct 15 '15 at 13:49