How write a new MatrixRank feature with symbolic computation

Question

The current MatrixRank is a slight foolish without any capacity of symbolic computation ,feature of Mathematica, like this:

(mat = Normal@SparseArray[{i_, i_} -> a, 5, b]) // MatrixForm

MatrixRank[mat]
(*5*)

But actually we expect the result in mathematics is:

when a=b=0,rank(mat)=0
when a=b≠0,rank(mat)=1
when a+4b=0,rank(mat)=4
when a≠b&&a≠-4b,rank(mat)=5

I'd like to be Solve's result:

In[1]:= Solve[x^2 + y^2 + x == 1, y, Reals]

Out[1]= {{y -> 
   ConditionalExpression[-Sqrt[1 - x - x^2], 
    1/2 (-1 - Sqrt[5]) < x < 1/2 (-1 + Sqrt[5])]}, {y -> 
   ConditionalExpression[Sqrt[1 - x - x^2], 
    1/2 (-1 - Sqrt[5]) < x < 1/2 (-1 + Sqrt[5])]}}

It will give a ConditionalExpression for every result.And I think the Mathematica can do it via some solution.like following we can find some condition for this:

But I don't know what I should to do next for this.So help Mathematica,help me to improve or rewrite the MatrixRank,give some thinking,please.

First you will want to know what makes eigenvalues vanish. That can be found as follows. `In[10]:= roots = x /. Solve[CharacteristicPolynomial[mat, x] == 0, x]
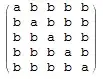
Out[10]= {a - b, a - b, a - b, a - b, a + 4 b}. Next take all subsets and invoke something likeSolve[subset==0&&Complement[set,subset]!=0]` to find all cases where rank= #subset. In this case of course it simplifies since there is a repeated root, but this should give the general idea. — Daniel Lichtblau, Oct 15 '15 at 14:30
Can you post an arranged answer that I can accept it?And it will be helpful to another to read it. — yode, Oct 15 '15 at 14:51
One other possibility is similar to Daniel's solution, except that what I had in mind was to use LUDecomposition[], and then do the checks described by Daniel on the diagonal entries of the upper triangular factor. — J. M.'s missing motivation, Oct 15 '15 at 15:15
The approach by @J.M. might be more sensible since it reduces the possibility of working over an algebraic extension to the case of finally checking subsets. But I think there is then a new complication, of rechecking such cases to see what happens next (heuristic reason: if a potential pivot were to vanish, that does not mean there is no other possible pivot). — Daniel Lichtblau, Oct 15 '15 at 15:27

score 9 · Answer 1 · answered Oct 15 '15 at 15:23

This is not a complete solution but should provide a start. In the special case of a square matrix we can determine conditions on rank by determining where specific numbers of eigenvalues vanish. We show how to set this up using the example from the post.

mat = Normal@SparseArray[{i_, i_} -> a, 5, b]

(* Out[17]= {{a, b, b, b, b}, {b, a, b, b, b}, {b, b, a, b, b}, {b, b, b,
   a, b}, {b, b, b, b, a}} *)

roots = x /. Solve[CharacteristicPolynomial[mat, x] == 0, x]

(* Out[18]= {a - b, a - b, a - b, a - b, a + 4 b} *)

To proceed from here one could do as follows.

For each subset sroots of roots, do Reduce[Flatten[Thread[sroots==0],Thread[Complement[roots,sroots]!=0]]]. If sroots has size n then this gives a set of conditions for the rank to be exactly n.

This will take some real work to make efficient in those cases where, as above, there are (generically) repeated roots.

Does x /. Solve[CharacteristicPolynomial[mat, x] == 0, x] do anything that Eigenvalues[mat] can't do? — J. M.'s missing motivation, Oct 15 '15 at 16:03
sol = SolveValues[CharacteristicPolynomial[mat, x] == 0, x]; Piecewise[ Table[{n, Reduce[n == Total[Boole[Thread[sol != 0]]]]}, {n, 5, 0, -1}], Indeterminate] can do indeed, but CharacteristicPolynomial require a square matrix — yode, Jan 24 '22 at 06:21

mikea · Answer 2 · 2020-03-24T00:16:55.077

3

Max Rank

I use the following function to check if the matrix is of a maximum rank:

(* Max Rank? *)
MRQ[m_] := Minors[m, Min[Dimensions[m]]] != 0;

Usage example:

Reduce[MRQ[{{3 x^2, 3 y^2, 3 z^2}, {1, 1, 1}}], {x, y, z}]

results in:

x^2 - y^2 != 0 || x^2 - z^2 != 0 || y^2 - z^2 != 0

or

Solve[! MRQ[{{3 x^2 - 6 y, -6 x + 2 y}}], {x, y}]

in

{{x -> 0, y -> 0}, {x -> 6, y -> 18}}

edited Mar 24 '20 at 00:16

answered Mar 24 '20 at 00:11

mikea

379
1
5

1

Note that the question asks for something to compute the matrix's rank, not to check if the matrix's rank is maximal. – J. M.'s missing motivation Mar 24 '20 at 01:10

yode · Accepted Answer · 2022-01-24T06:02:37.627

MatrixRankSym[mat_] := Module[{smallDim, zero, full},
  If[AllTrue[Flatten[mat], NumberQ], Return[MatrixRank[mat]]];
  smallDim = Min[Dimensions[mat]];
  zero = Reduce[Thread[Flatten[mat] == 0]];
  full = If[SquareMatrixQ[mat], Reduce[Det[mat] != 0], 
    Reduce[Or @@ Thread[Flatten[Minors[mat, smallDim]] != 0]]];
  If[smallDim >= 2, 
   Piecewise[
    Join[{{smallDim, full}}, 
     Table[{dim, 
       Reduce[Or @@ Thread[Flatten[Minors[mat, dim]] != 0] && 
         And @@ Thread[Flatten[Minors[mat, dim + 1]] == 0]]}, {dim, 
       Range[smallDim - 1, 1, -1]}], {{0, zero}}], Indeterminate], 
   Piecewise[Join[{{0, zero}}, {{smallDim, full}}], Indeterminate]]]

Usage:

mat = Normal@SparseArray[{i_, i_} -> a, 5, b];
MatrixRankSym[mat]

mat2 = {{3 x^2, 3 y^2, 3 z^2}, {1, 1, 1}};
MatrixRankSym[mat2]

score 1 · Answer 4 · answered Apr 05 '17 at 01:10

Not perfect but a good start

Join[{#, MatrixRank[mat /. #]} & /@ 
  Flatten[{ToRules[
     Reduce[Det[mat] == 0, a]]}], {If[(fullRank = 
      Reduce[Det[mat] > 0, a, Reals]) =!= False, {fullRank, 5}, 
   Nothing]}]

{{a -> -4 b, 4}, {a -> b, 1}, {(b <= 0 && a > -4 b) || (b > 0 && (-4 b < a < b || a > b)), 5}}

But I don't know how to deal the case when rank is $0$

How write a new MatrixRank feature with symbolic computation

4 Answers4

Max Rank

Usage:

Linked