2

If 

f:= x^3 + y*x*z - z^2 + x*z

and if {{1,2,1},{2,7,8},{6,0,2},{9,1,1}} are points, how can I find the tangent plane to f at the four points in the same time.

I saw some codes to calculate the tangent , for example, 

tg[f_, x_, p_] := (f'[x] /. x -> p) (x - p) + f[p]
q = #^3 - 3 #^2 &;
Manipulate[
 Plot[{q[x], tg[q, u, m] /. u -> x}, {x, -3, 3}, PlotRange -> {-5, 5},
   Epilog -> {Red, PointSize[0.02], Point[{m, q[m]}]}], {m, -1, 1, 
  0.01}]

but I am confused this did not answer my question. Thanks for any help.

Jason B.
  • 68,381
  • 3
  • 139
  • 286
user12
  • 21
  • 1
  • 2
    Before you come to answering this question in Mathematica, can you map out a plan of how to solve this issue - some pseudocode? Mathematically, what would you need, which derivatives? And what do you mean exactly by "tangent" - a plane or a line? Do you know what the code you pasted does? – Jason B. Oct 23 '15 at 11:38
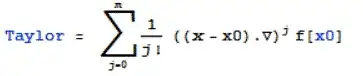
  • If f is a function of three variables, then wouldn't the tangent be three dimensional as well? I'm just thinking about the tangent to f[x] is a line, and the tangent to f[x,y] is a plane. – Jason B. Oct 23 '15 at 11:53
  • The solution would come from applying the technique here, which shows how to find the plane tangent to a surface, to four dimensions instead of three - sounds like a fun homework problem. – Jason B. Oct 23 '15 at 12:23
  • @Jason, yes, a hyperplane would be a 3D manifold. – J. M.'s missing motivation Oct 23 '15 at 13:01

3 Answers3

3

Taken from here and here

f := x^3 + y*x*z - z^2 + x*z

tangent[point_] := ({x, y, z} - point).(D[f, {{x, y, z}}] /. 
     Thread[{x, y, z} -> point]) + (f /. Thread[{x, y, z} -> point])

(thanks to J.M. for the improvement here)

You can get the tangent for the four points via

(tangent /@ {{1, 2, 1}, {2, 7, 8}, {6, 0, 2}, {9, 1, 1}}) // TableForm

enter image description here

Since this is a function of three variables, the only way I can think to plot it is using a ContourPlot3D

ContourPlot3D[
 Evaluate[tangent[{6, 0, 2}]], {x, -5, 5}, {y, -5, 5}, {z, -5, 5}]

enter image description here

Jason B.
  • 68,381
  • 3
  • 139
  • 286
  • 2
    A bit shorter: tangent[point_] := ({x, y, z} - point).(D[f, {{x, y, z}}] /. Thread[{x, y, z} -> point]) + (f /. Thread[{x, y, z} -> point]) Dot products and gradients are nice. :) – J. M.'s missing motivation Oct 23 '15 at 13:38
3

To illustrate points made in comments:

f[x_, y_, z_] := x^3 + y*x*z - z^2 + x*z
dat = {{1, 2, 1}, {2, 7, 8}, {6, 0, 2}, {9, 1, 1}};
tpl[x_, y_, z_, p_, q_, r_] := 
 With[{g = Grad[f[a, b, c], {a, b, c}] /. {a -> x, b -> y, c -> z}},
  g.{p - x, q - y, r - z} == 0
  ]
func[a_, b_, c_] := 
 Show[ContourPlot3D[
   f[x, y, z] == f[a, b, c], {x, -10, 10}, {y, -10, 10}, {z, -10, 10},
    Mesh -> False, PlotLabel -> f[x, y, z] == f[a, b, c]],
  Graphics3D[{Red, PointSize[0.03], Point[{a, b, c}]}]]

The surfaces through points and the tangent plane to points:

planes = ContourPlot3D[#, {x, -10, 10}, {y, -10, 10}, {z, -10, 10}, 
     Mesh -> None, 
     ContourStyle -> {Pink, Opacity[0.5]}] & /@ (tpl[##, x, y, z] & @@@
      dat);
surfaces = func @@@ dat;
Grid[Partition[MapThread[Show[#1, #2] &, {surfaces, planes}], 2]]

enter image description here

This could have been done in a much neater way but I hope supports comments.

ubpdqn
  • 60,617
  • 3
  • 59
  • 148
  • @JasonB I think we are doing the same thing in slightly different ways. I am just plotting surface that passes through given point, the point and using the gradient as normal vector for tangent plane – ubpdqn Oct 23 '15 at 13:40
  • 1
    Yeah, I see that now. Still incredibly hard to visualize four-dimensional objects - even as contour plots. Even here - how do we see that the planes are tangential to the surfaces? They seem to go through them – Jason B. Oct 23 '15 at 13:46
  • @JasonB I cannot visualise 4D or above in my imagination but the points let us plot a contour in 3D space and then we can play a bit...:) – ubpdqn Oct 23 '15 at 13:51
  • Right - so I guess it's true that the 3D contours to a tangent hyperplane are not tangent to 3D contours of the surface, even when the same contour value is used. (you can tell I'm not a mathematician or I'd have known that I suppose) – Jason B. Oct 23 '15 at 13:53
  • @Jason: "Even here - how do we see that the planes are tangential to the surfaces?" I can't implement the idea right now, but maybe either you or ubpdqn can pursue it. Consider a lower dimensional analogy: if you slice a usual 3D surface and its tangent plane with a plane that passes through the point of tangency, you will see the image of some curve and some line that is tangent to it. It looks to me that it can be done for higher dimensions. (I used an idea like that here.) – J. M.'s missing motivation Oct 23 '15 at 13:56
  • @J.M. Something like "Consider a sphere in R^3 and find a line tangent to two points at the same time"? :) – Dr. belisarius Oct 23 '15 at 14:28
  • @bel, no, that's an impossible problem; very different species. :P – J. M.'s missing motivation Oct 23 '15 at 14:31
  • @J.M. That's what is written in the question :) – Dr. belisarius Oct 23 '15 at 14:33
0

For the sake of completeness, it applies the general Taylor formula:

enter image description here

She can be coded as follows (m = 1 -> tangent):

taylorPolynom[point_] := Sum[
  1/j! Nest[(vars - point).# &, 
     D[f[vars], {vars, j}] /. Thread[vars -> point], j], {j, 0, m}]

vars = {x, y, z};
f[vars_] = x^3 + y*x*z - z^2 + x*z;
m = 1;

And with the points we get:

taylorPolynom /@ {{1, 2, 1}, {2, 7, 8}, {6, 0, 2}, {9, 1,1}} 
{6 (-1 + x) + y + z,
 72 + 76 (-2 + x) + 16 (-7 + y),
 224 + 110 (-6 + x) + 12 y + 2 (-2 + z),
 746 + 245 (-9 + x) + 9 (-1 + y) + 16 (-1 + z)}

The same result as the above solutions, but this solution is generally valid for each dimension.