1

Related to Gerhard's question about ascii plots. On the SeqFan mailing list was suggested to plot an integer sequence this way:

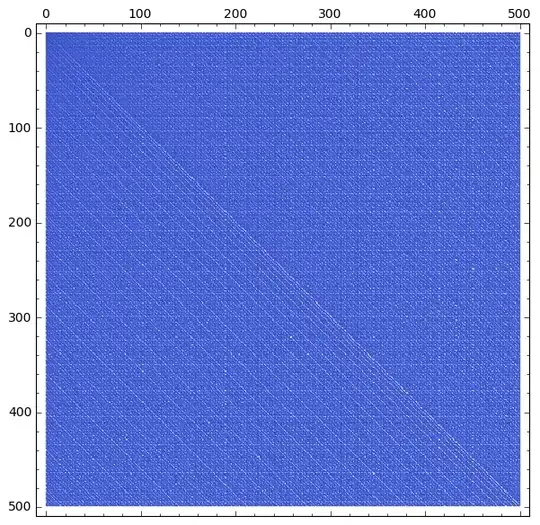
Let $F(x,y)= (x+y) (x+y+1)/2+y$ be the Cantor pairing. To plot an integer sequence $a(n)$, for a point $(x,y)$ compute $a(F(x,y))$ and assign color to the integer, e.g. in grayscale smaller is darker, for RGB/HSV there are other choices to map to color.

When $a(n)=\sigma_0(n)$ where $\sigma_0(n)$ is the number of divisors of $n$, the 2D plot shows some structure (hopefully not caused by visual artifacts).

Is there an explanation for the structure in the plot?

Color plot of $\sigma_0(F(x,y))$, smaller is darker (grayscale is quite similar):

sigma_0 and cantor pairing

When examining the integer values there are some large diagonals indeed.

Community
  • 1
joro
  • 24,174

1 Answers1

2

Have you tried to find an explanation?

The diagonals correspond to numbers $F(x,x+j).$ Every eighth one has $F(x,x+8k)=2x(x+1)+4(8k^2+4xk+3k).$ Since these are all multiples of $4$ that is already a boost.

$F(x,x+1)=2(x+1)^2.$ This is the case $q=0$ of $F(x,x-(q^2-1))=2(x-\binom{q}{2}+1-q)(x-\binom{q}{2}+1).$ So these are all pretty composite and every $q$th member is a multiple of $2q^2.$ Probably you can prove that there are no other diagonals which factor algebraically.

You will find the horizontal lines $F(\binom{j}{2}-1,y)$ worth examining.

Your image also shows possible anti-diagonals $F(x,k-x)$ but I will leave that for someone else to examine (I did not immediately see anything).

A few later comments: Along any line (the ones easily seen are horizontal, vertical and slope $\pm 1$) the values are periodic $\mod p.$ Certain dark lines can be explained by verifying that no member can divide by a small prime. I seem to recall that the lines $F(x,x-(q^2-3))$ contain no multiples of $2,3,5$ and in some cases no multiples of any prime under $30$. Some of this shows in the graphic and some not as much.

Aaron Meyerowitz
  • 30,015