Is there always a maximum anti-rectangle with a corner square?

Question

Let $C$ be an axis-parallel orthogonal polygon with a finite number of sides. Define an anti-rectangle in $C$ as a set of small squares in $C$, such that no two of them are covered by a single large rectangle in $C$. Define a maximum anti-rectangle as an anti-rectangle that contains a maximum number of squares. For example, the following L-shape has a maximum anti-rectangle with 2 squares:

The following C-shape has a maximum anti-rectangle with 3 squares:

And the following shape has a maximum anti-rectangle with 5 squares:

When I try to build an anti-rectangle, I usually start with putting squares in the corners of $C$, because intuitively, the corners have the least chance of being covered by a rectangle. This raises the following conjecture:

For every $C$, there is a maximum anti-rectangle, which contains a corner square.

(- a corner square is a square with at least two adjacent sides that are in the boundary of $C$).

I found in Chaikan et al (1981) a proof that the conjecture is true when $C$ is linearly-convex (- contains every vertical or horizontal line that connects two of its points; like the L-shape above).

Their proof is not valid when $C$ is not linearly-convex, but I also cannot find a counter-example. What do you say?

---

CONCLUSION: Many thanks to all repliers. The conjecture is false when the polygon may have holes (as shown by dmotorp). It is true when the polygon is hole-free (as proven by Nick Gill and mhum).

UPDATE: I cited this thread in the following working paper. I hope it will be accepted.

Answer 1

I think the answer is YES .

Suppose that $d$ is a little square that lies in exactly one maximal subrectangle $C$ in the polygon. Then any anti-rectangle contains exactly one little square in $C$. We can replace this square by $d$ and still have an anti-rectangle.

So one is required to prove the following:

Proposition: In every hole-free polygon, there exists a corner square that lies in exactly one maximal subrectangle.

Sketch of proposed proof: Observe that as one moves clockwise around the perimeter of the polygon, one must go either left or right at various stages. One obtains a sequence: $R,R,L, R, L \cdots$ and it is clear that the number of $R$'s is 4 more than the number of $L$'s.

Motivating observation: suppose that in this sequence one has three $R$'s in a row. Then the corner corresponding to the middle $R$ will lie in a unique maximal subrectangle. (Edit: as commeters have pointed out - this isn't true. But it's not used in what follows.)

The problem is that one may not have three $R$'s in a row - one does, however, have at least $2$ $R$'s in a row. Let us examine whether or not one of the two corresponding corners lies in a unique maximal subrectangle.

(Here my sketch will get icky, because I don't have Joseph O'Rourke's excellence in drawing pictures...)

I claim that the only way both of these $R$-corners can fail to lie in a maximal sub-rectangle, is if the piece of the polygon 'opposite' the corners has some kind of crenellation, i.e. two knobs sticking out opposite each corner. These might not be 'smooth' - there could be many many bends in them but, still, if one gives this a little thought it becomes quite clear that this can only happen if `opposite' the edge between the two consecutive $R$-corners one has two consecutive $L$-corners.

Now we know that this cannot happen to all consecutive $R$-corners, because the number of $R$-corners exceeds the number of $L$-corners by $4$.

(Edit: @mhum pointed out that one may have several pairs of $R$-corners opposing a single pair $\mathcal{P}$ of $L$-corners. However if this were to happen, then each pair of $R$-corners would necessarily be separated by a pair of $L$-corners that were also opposite to $\mathcal{P}$, and so our count would not be affected.)

QED

Answer 2

The answer is negative if you allow holes. Consider a 5 times 5 square with its center missing. Then the 4 squares adjacent to the center form an antirectangle, but any antirectangle that contains a corner square has at most three squares.

Answer 3

This answer is more or less just a formalization of the intuition put forward by Nick Gill in his answer. The beginning parts are mostly just formalities, so you can probably skip down to the diagram.

Let $C$ be an axis-aligned orthogonal polygon. Following Chaikan et al., we'll consider $C$ as a union of squares. For any square $x \in C$, we define $$R(x) = \{ y \in C \;|\; \exists \text{ a rectangle in $C$ containing $x$ and $y$}\}$$ with the understanding that $x\in R(x)$. Next, we define a pre-order $\leq$ on $C$ by $$ x \leq y \iff R(x) \subseteq R(y)$$

Let $x$ and $y$ form an anti-rectangle and let $R(z) \subseteq R(x)$. Then, we can show that $z$ and $y$ also form an anti-rectangle. It follows that given an anti-rectangle $\{x_1, x_2, \ldots, x_k\}$, we can find another anti-rectangle $\{x_1', x_2', \ldots, x_k'\}$ of equal cardinality where each $x_i'$ is chosen to be a minimal element such that $x_i' \leq x_i$. In fact, we can construct a maximum anti-rectangle by selecting one representative from each of the minimal equivalence classes (defined in the usual way by the pre-order).

It now remains to show that if $C$ does not contain any holes, then there exists at least one minimal corner square. We will actually show slightly more: that there is at least one corner square $x$ on a "support edge" (by Chaikan et al's terminology) such that $R(x)$ is a rectangle. Observe that if $R(x)$ is a rectangle, then $x$ is minimal; we leave as an exercise for the reader to construct an example that shows that the converse is false.

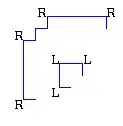
Each edge in $C$ can be categorized by the squares at its endpoints. An edge can have either two, one, or zero corners at its endpoints. In the terminology laid out in Nick Gill's answer, these would correspond to $RR$, $RL$ (or $LR$), and $LL$ edges respectively (also, $RR$ edges correspond to "support edges" in Chaikan et al's terminology).

The key lemma we will need is that if $C$ is a simple, orthogonal polygon then it has strictly more $RR$ edges than $LL$ edges. First, we'll take as given that there are strictly more $R$ corners than $L$ corners (again, as defined in Nick Gill's answer) in $C$. Let $rr$, $ll$, and $rl$ be the number of $RR$, $LL$, and $RL$ edges. We will now try to count the number of each type of corner via counting each edge. Each $RR$ edge we'll count as two $R$ corners, each $LL$ edge as two $L$ corners, and each $RL$ edge as one $R$ and one $L$ corner. Counting in this way, we end up counting each corner exactly twice. So, we have $2r = 2rr+rl$ and $2l = 2ll+rl$. Thus, $0 < 2r - 2l = 2rr - 2ll$ and hence there are strictly more $RR$ edges than $LL$ edges.

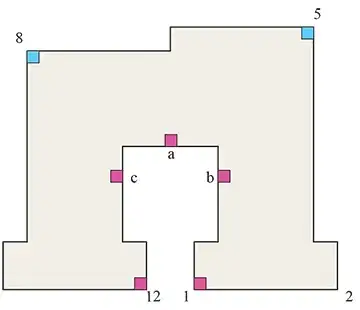
Consider the following diagram of an $RR$ edge:

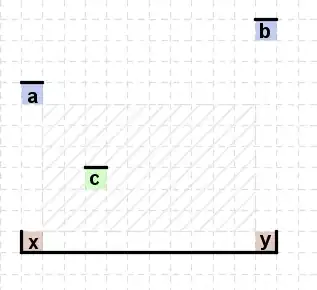
The heavy black lines indicate known boundaries of $C$. The red squares, $x$ and $y$ are the corners of the $RR$ edge. The blue squares $a$ and $b$ are the edge squares directly above $x$ and $y$ respectively (i.e.: all the squares between $x$ and $a$ and between $y$ and $b$ are interior squares).

If there were no edge squares in the shaded region, then $R(x)$ would be a rectangle and we would be done. So, let $c$ be an edge square in the shaded region. Furthermore, we choose $c$ to one of the edge squares closest to the $xy$ edge (i.e.: $c$ is one of the southernmost edge squares in the shaded region). Call the edge corresponding to $c$, $E$. Note that while there may be more than once such edge, for our purposes we will only need to choose one.

We now infer that $E$ must be an $LL$ edge. By construction of the shaded region, the endpoints of $E$ must lie inside the shaded region (otherwise, it would violate one of the clear paths between $x$ and $a$ or $y$ and $b$). Thus, if one of the endpoints of $E$ were a corner, it would contradict the choice of $c$ as one of the southernmost edge squares. Finally, we see that $E$ can be uniquely identified in this way with the $RR$ edge corresponding to $xy$. Otherwise, it would once again contradict the choice of $c$ as closest to $xy$.

So, we conclude that any $RR$ edge where the corners are not minimal can be uniquely identified with an $LL$ edge. Since there are more $RR$ edges than $LL$ edges, one of them must contain a minimal corner.

Answer 4

Could you please clarify your definitions via the example polygon below?
   
Is $\{a,b,c,1,12\}$ an antirectangle of size $5$? Is this a maximal antirectangle? What is a largest antirectangle that includes a corner in this example?

---

Again, just illustrating the definitions, here is a maximal antirectangle, following the OP's comments:
   

Answer 5

Here is a very very simple observation, inspired by Nick's three R's in a row approach.

Claim: If there is a maximal rectangle Q in C, such that C\Q is connected, then there is a corner of C (and also Q) that must be in every maximal antirectangle.

Proof: This follows simply by noticing that the boundary of C and Q intersect each other in a continuous arc, so if the corners of Q are denoted abcd, then (without loss of generality) ab and bc are also sides of C and so are the beginning of the segments ad and cd. In this case b can see at most as much as any other point in Q.

Of course, there are polygons without such a Q, e.g., a cross.

Answer 6

Here is an approach which is incomplete, but might be combined with Nick Gill's approach to yield something nice.

I 'll let others do the routine of formalizing the notions of cover, orthogonal cover by rectangles, reduced cover. The key idea is that a reduced cover covers a polygon by axis aligned rectangles, that it does so with finitely many such, that each rectangle is as large as can be in the cover, and that there is no redundancy, which gives that a maximal anti rectangle can be constructed from a reduced cover, and an anti rectangle can produce a cover which can be reduced to one that produces another anti rectangle containing the first anti rectangle. (The map from AR to RC to AR seems important, but is not necessary.)

Now note that we are trying to find an RC such that a polygon corner is covered by only one rectangle. Consider the directed inclusion graph with rectangles as vertices and edges joining a to b if b contains a corner of a. I think the graph has a cycle only if the polygon has a hole, and that otherwise there is a degree 1 vertex. Perhaps someone can prove this, from which the original poster's conjecture follows.

Answer 7

This is an attempt to complement Nick Gill's answer. If it is correct (I am not sure), it should be merged into his answer.

Proposition: In every hole-free polygon, there exists a corner square that lies in exactly one maximal subrectangle.

Proof: Observe that as one moves clockwise around the perimeter of the polygon, one must go either left or right at various stages. One obtains a sequence: $R,R,L, R, L \cdots$ and it is clear that the number of $R$'s is 4 more than the number of $L$'s. Therefore there must be a pair of two adjacent $R$'s.

Assume w.l.o.g. that there is such a pair such that the side between the corners faces west. Consider the maximal rectangle that covers the two $R$ corners (red in the pictures below). This rectangle must run into at least one eastern side. There are two cases:

Case A: The eastern side is connected to an $R$ corner adjacent to the $RR$ pair at the north or south:

In this case, the middle $R$ corner is contained in exactly one maximal rectangle (the red one) and we are done.

Case B: The eastern side is between two adjacent $L$ corners:

By the construction, it is clear that this $LL$ pair cannot be used in the same way with any other $RR$ pair.

Now we know that this cannot happen to all consecutive $R$-corners, because the number of $R$-corners exceeds the number of $L$-corners by $4$.

EDIT: I am not sure about the latter counting argument. What if there is a sequence LLL, such that the first LL pair matches an RR pair, and the second LL pair matches a disjoint RR pair?