Can a row of five equilateral triangles tile a big equilateral triangle?

Question

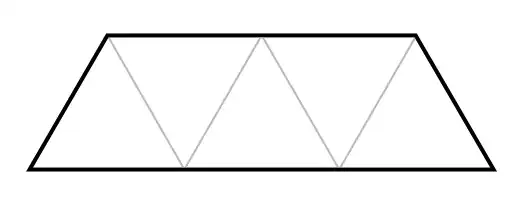
Can rotations and translations of this shape

perfectly tile some equilateral triangle?

---

I originally asked this on math.stackexchange where it was well received and we made some good progress. Here's what we learnt:

• Because the area of the triangle has to be a multiple of the area of the tile, the triangle must have side length divisible by $5$ (where $1$ is the length of the short edges of the tile).
• The analogous tile made of three equilateral triangles can tile any equilateral triangle with side length divisible by three.
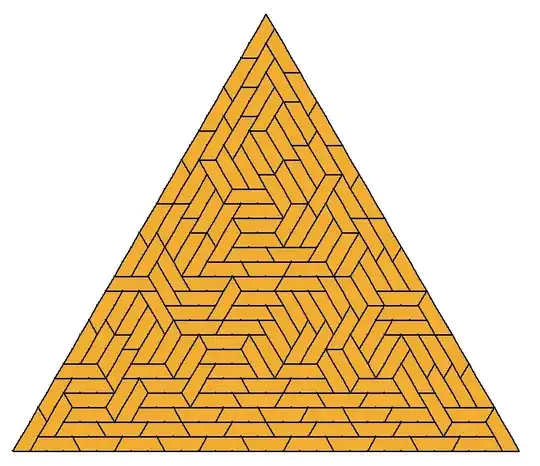
• There is a computer program, Burr Tools, which was designed to solve this kind of problem. Josh B. used it to prove by exhaustive search that there is no solution when the side length of the triangle is $5$, $10$, $15$, $20$ or $25$. The case of a triangle with side length $30$ would take roughly ten CPU-years to check using this method.
• Lee Mosher pointed me in the direction of Conway's theory of tiling groups. This theory can be used to show that if the tile can cover an equilateral triangle of side length $n$ then $a^nb^nc^n=e$ in the group $\left<a,b,c\;\middle|\;a^3ba^{-2}c,a^{-3}b^{-1}a^2c^{-1},b^3cb^{-2}a,b^{-3}c^{-1}b^2a^{-1},c^3ac^{-2}b,c^{-3}a^{-1}c^2b^{-1}\right>$. But sadly it turns out that we do have that $a^nb^nc^n=e$ in this group whenever $n$ divides by $5$.
• In fact one can use the methods in this paper of Michael Reid to prove that this tile's homotopy group is the cyclic group with $5$ elements. I think this means that the only thing these group theoretic methods can tell us is a fact we already knew: that the side length must be divisible by $5$.
• These group theoretic methods are also supposed to subsume all possible colouring arguments, which means that any proof based purely on colouring is probably futile.
• The smallest area that can be left uncovered when trying to cover a triangle of side length $(1,\dots,20)$ is $($$1$$,\,$$4$$,\,$$4$$,\,$$1$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$,\,$$6$$,\,$$4$$,\,$$4$$,\,$$6$$,\,$$5$$)$ small triangles. In particular it's surprising that when the area is $1\;\mathrm{mod}\;5$ one must sometimes leave six triangles uncovered rather than just one.
• We can look for "near misses" in which all but $5$ of the small triangles are covered and in which $4$ of the missing small triangles could be covered by the same tile. There's essentially only one near miss for the triangle of side $5$, none for the triangle of side $10$ and six (1,2,3,4,5,6) for the triangle of side $15$. (All other near misses can be generated from these by rotation, reflection, and by reorienting the three tiles that go around the lonesome missing triangle.) This set of six near misses are very interesting since the positions of the single triangle and the place where it "should" go are very constrained.

I'd also be interested in learning what kind of methods can be used to attack this sort of problem. Are there any high-level approaches other than the tiling groups? Or is a bare hands approach most likely to be successful?  

Answer 1

It seems that one can color a 15-15-15-30 trapezoid with the given tiles. Here is a picture (sorry about adjacent figures that are the same color, I used random colors so hopefully there are no ambiguities):

In particular, OP pointed out that these scaled 1-1-1-2 trapezoids can tile any equilateral triangle whose side length is a multiple of three. So the original tile can tile any equilateral triangle whose side length is a multiple of 45.

I bet we didn't see answers for smaller $n$ due to an Aztec-diamond-like boundary condition with the corners.

Answer 2

Since nobody has posted it, here's the smallest triangle tilable by the 'straight pentiamond', ie a side-30 triangle. Simple backtracking program, takes 0.5 seconds to show no tilings of the side-20 triangle, 4:39 for the side 25. Took 12 minutes to find 120 tilings for the side-30 before I stopped it.

Answer 3

There was a conference in July 2007 at the University of Minnesota—Duluth in honor of Joseph Gallian's 65th birthday. At that conference, Michael Reid gave a talk about tilings, and among other things, he discussed this exact problem. Reid has shown that this "pentiamond" tiles all equilateral triangles with side length ≥30 (provided the side length is divisible by 5, of course). He has also shown that it is a "rep-tile": it tiles a copy of itself, scaled by a factor of k, if and only if k ≥ 11.

Naturally, one can generalize this problem by considering tiles consisting of 7, 9, 11, … triangles in a row. Reid conjectures that every such tile tiles all sufficiently large equilateral triangles whose area is a multiple of the area of the tile, as well as all sufficiently large scaled copies of itself. He has found a tiling of an equilateral triangle for the heptiamond case, but does not know what the smallest such triangle is.

It seems that Reid has never published these results. I've emailed him to see if he can supply more details of the tilings mentioned here.

Answer 4

I do not know whether the triangular region with size a multiple of 5 is tileable in general, but I can address the question in the last paragraph:

I'd also be interested in learning what kind of methods can be used to attack this sort of problem. Are there any high-level approaches other than the tiling groups?

Apparently, one can get extra mileage out of coloring arguments by considering semigroups rather than groups. Here is a conceptual proof, based on a coloring argument with 6 colors, that the size 5 triangular region is not tileable. After the preliminary work is done, the actual proof is very short. (The setup is completely general, but I have not figured out yet whether this method would be fruitful for proving or disproving tileability for larger sizes divisible by 5.)

We imagine that the region is broken into small triangles, which we call cells. Per usual conventions, "tile" means a congruent copy of the given shape with 5 cells ("prototile") located anywhere in the region.

Definition. A color is an element of $\{1,2,3,4,5,6\}$ (viewed modulo 6). A coloring is an assignment of a color to each cell of the region.

Let us situate the triangular region of size $n$ so that the base of the big triangle is horizontal and the triangle is above it. This region is divided into horizontal strips formed by small triangles with alternating orientations, with $2n-1, 2n-3, \ldots, 1$ cells, each strip zigzagging from the left side of the region to the right.

Proposition 1. There is a periodic coloring of a triangular region of any size with the following properties:

<ol>
<li><p>The lower left corner cell is colored $1$.</p></li>
<li><p>In every horizontal strip, the colors increment by $1$ as one zigzags through its cells from left to right. </p></li>
<li><p>The colors of two cells sharing a horizontal side differ by $3$.</p></li>
<li><p>For each tile situated anywhere in the region, its cells have distinct colors; let us label the tile (or its position) by the unique color which does <em>not</em> occur. </p></li>
</ol>

Example of such a coloring where n=5:

Proposition 2. For size 5 triangular region, the distribution of the colors is as follows: ($1^5 2^4 3^5 4^3 5^5 6^3$). Furthermore, the tiles containing corner cells are labelled $4$ if oriented clockwise and $6$ if oriented counterclockwise.

It is clear that in any tiling of a triangular region, each corner cell is covered by a unique tile. Moreover, if the region has size 4 or more, these tiles are distinct. Let us call them corner tiles. Each corner tile has one of two possible orientations (clockwise and counterclockwise).

Proposition 3. In any tiling of size 5 triangular region, the three corner tiles are either all oriented clockwise or all oriented counterclockwise.

Since 5$<$3+3, if two corner tiles had the opposite orientation, they would overlap.

---

Proof of non-tileability for size 5 triangular region: Since the region has 25 cells, any tiling has 5 tiles. Labelling them as in Proposition 1, by Proposition 2 there are exactly 2 tiles labelled $4$ and 2 tiles labelled $6$. This contradicts Proposition 3, because either all 3 corner tiles are labelled $4$ or they are all labelled $6$.

---

The main obstacle to generalizing this argument to larger size triangular regions is that since the corners of the region would be too far apart, Proposition 3 does not generalize. Clearly, one would need tighter control over how tiles are situated in the middle of the region. Perhaps, different colorings (or even combinations of colorings) can be exploited. Nonetheless, even in this form, Proposition 1 and the analog of Proposition 2 for a given size region impose some restrictions on potential locations of the tiles. For example, for size 10 there is a unique tile labeled $1$, a fact which can perhaps be exploited to drastically decrease search space of a brute force search algorithm.

Answer 5

This does not answer the question, but I would like to update an assertion in the post.

A triangle of side 4 can hold three of the tiles with a hole in the center. 25 of these patterns can be repeated to cover all but 25 unit triangles of a triangle of side 20. Of course, one can use this for near optimal (if not optimal) partitions of triangles of side length 4k for k a positive integer.

Unless you are familiar with the group theoretic methods mentioned in the post above, I would not use them to dismiss coloring attempts. A pure argument by coloring may not work, but it may point to an argument that does. The checkerboard coloring aids me in a proof that the triangle of side 5 does not admit a tiling with the given tile.

Edit 2017.04.13. GRP: I will toss out an idea which comes from shearing the triangle into half a square. Perhaps it will lead somewhere.

Do a "square checkerboard" coloring of the triangle. Starting from the top, color the first two rows of triangles black, then the next two white, then the next two black. Another way to state this is to color the top diamond (two triangles joined by an edge) black, the next two top diamonds white, the next top three black, on down to the bottom triangles which will be black if n is odd, and white if n is even. Each tile covers either one white diamond and one black diamond and a half of some color, or it covers three halves of one color and two halves of another.

The idea is that this coloring produces more white diamonds than black diamonds when n is odd, and vice versa when n is even, as well as n triangles of one color. This should imply that a certain number of the tiles have to be oriented in a horizontal direction, and the hope is that (as five is not a multiple of 3) that this will lead to contradicting the existence of a tiling. End Edit 2017.04.13. GRP.

Gerhard "Give Simple Intuition A Chance" Paseman, 2017.04.13.