How is this bicycle model in Robotics Vision & Control derived? And is its equation missing something?

Question

I'm reading Robotics, Vision and Control, on page 108 it has following equations:

$$\rho=\sqrt{\Delta^2_x+\Delta^2_y}$$ $$\alpha = \tan^{-1}\frac{\Delta_y}{\Delta_x}-\theta$$ $$\beta = -\theta-\alpha$$

How does it go from the above to the following equations?

$$\pmatrix{ \dot{\rho}\\ \dot{\alpha}\\ \dot{\beta}} = \pmatrix{ -\cos \alpha & 0\\ \frac{\sin \alpha}{\rho} & -1\\ -\frac{\sin \alpha}{\rho} & 0 }\pmatrix{v \\ \omega }\text{, if } \alpha \in \left(-\frac{\pi}{2}, -\frac{\pi}{2}\right] $$

$$v=k_p\rho$$

$$\omega=k_\alpha \alpha+k_\beta \beta$$

$$\pmatrix{ \dot{\rho}\\ \dot{\alpha}\\ \dot{\beta}} = \pmatrix{ -k_\rho \cos \alpha\\ k_\rho \sin\alpha - k_\alpha \alpha -k_\beta \beta\\ -k_\rho \sin \alpha } $$

Shouldn't $\dot{\rho} = -k_\rho \rho \cos\alpha$ ?

Answer 1

OK, I'm working from the 1st edition of the book, so section 4.2.4 of my edition starts on page 75, but the text appears otherwise to be the same.

---

Initially, the book re-writes the equations of motion of the robot, given earlier as Eq. 4.2:

$ \dot x = \nu cos \theta $

$ \dot y = \nu sin \theta $

$ \dot \theta = \frac {\nu} {L} tan \gamma $

in matrix form:

$ \begin{pmatrix} \dot x \\ \dot y \\ \dot \theta \end{pmatrix} = \begin{pmatrix} cos \theta & 0 \\ sin \theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix} $

---

These equations are then transformed into polar coordinate form using the notation from the following figure (figure 4.12 in my edition, yours may vary):

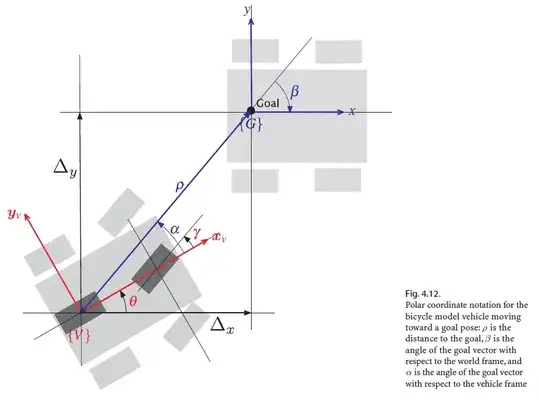
From this figure, we obtain your first set of equations:

$ \rho = \sqrt {\Delta ^{2} _{x} + \Delta ^{2} _{y}} $

$ \alpha = tan ^{-1} \frac {\Delta _{y}} {\Delta _{x}} - \theta $

$ \beta = - \theta - \alpha $

---

Next, we apply the chain rule. Multiply both sides of Eq 4.2 by the Jacobian of the coordinate transformation, J.

There are a couple of ways to obtain the Jacobian, J. Either differentiate the forward map to get

$ J = \begin{pmatrix} {\frac {\Delta _{x}} {\sqrt {\Delta ^{2} _{x} + \Delta ^{2} _{y}}}} & {\frac {\Delta _{y}} {\sqrt {\Delta ^{2} _{x} + \Delta ^{2} _{y}}}} & 0 \\ -{\frac {\Delta _{y}} {{\Delta ^{2} _{x} + \Delta ^{2} _{y}}}} & {{\frac {\Delta _{x}} {{\Delta ^{2} _{x} + \Delta ^{2} _{y}}}}} & -1 \\ {\frac {\Delta _{y}} {{\Delta ^{2} _{x} + \Delta ^{2} _{y}}}} & -{{\frac {\Delta _{x}} {{\Delta ^{2} _{x} + \Delta ^{2} _{y}}}}} & 0 \end{pmatrix} = \begin{pmatrix} -\cos\beta & \sin\beta & 0 \\ -{\frac {\sin \beta} {\rho}} & -{\frac {\cos \beta} {\rho}} & -1 \\ {\frac {\sin \beta} {\rho}} & {\frac {\cos \beta} {\rho}} & 0 \end{pmatrix} $

Alternatively, since we can write the inverse as:

$ \Delta _{x} = -\rho\cos(-\beta) = -\rho\cos\beta $

$ \Delta _{y} = -\rho\sin(-\beta) = \rho\sin\beta $

$ \theta = -(\alpha + \beta) $

we could write this in matrix form and differentiate to get:

$ \begin{pmatrix} -\cos \beta & 0 & \rho \sin \beta \\ \sin\beta & 0 & \rho \cos \beta \\ 0 & -1 & -1 \end{pmatrix} $

and then invert to obtain J:

$ J = \begin{pmatrix} -\cos\beta & \sin\beta & 0 \\ -{\frac {\sin \beta} {\rho}} & -{\frac {\cos \beta} {\rho}} & -1 \\ {\frac {\sin \beta} {\rho}} & {\frac {\cos \beta} {\rho}} & 0 \end{pmatrix} $

---

$ J \begin{pmatrix} cos \theta & 0 \\ sin \theta & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix} = \begin{pmatrix} -\cos \beta \cos \theta + \sin \beta \sin \theta & 0 \\ - \frac {1} {\rho} (\cos \beta \sin \theta + \sin \beta \cos \theta) & -1 \\ \frac {1} {\rho} (\cos \beta \sin \theta + \sin \beta \cos \theta) & 0 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix} $

Simplifying and then substituting $ \theta = -(\alpha + \beta) $ gives:

$ = \begin{pmatrix} - \cos (\beta + \theta) & 0 \\ - \frac {1} {\rho} \sin (\beta + \theta) & -1 \\ \frac {1} {\rho} \sin (\beta + \theta) & 0 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix} = \begin{pmatrix} - \cos \alpha &0 \\ {\frac {\sin \alpha} {\rho}} & -1 \\ - {\frac {\sin \alpha} {\rho}} & 0 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix} $

---

So, we can write:

$ \begin{pmatrix} \dot \rho \\ \dot \alpha \\ \dot \beta \end{pmatrix} = \begin{pmatrix} -cos \alpha & 0 \\ \frac {sin \alpha} {\rho} & -1 \\ -\frac {sin \alpha} {\rho} & 0 \end{pmatrix} \begin{pmatrix} \nu \\ \gamma \end{pmatrix}, \text { if } \alpha \in \begin{pmatrix} -\frac {\pi} {2} , \frac {\pi} {2} \end{pmatrix} $

Which is your second equation.

---

The equations

$ \nu = k _{\rho} \rho $

$ \gamma = k _{\alpha} \alpha + k _{\beta} \beta $

are the linear control law which, when applied to the equation we just derived gives us:

$ \begin{pmatrix} \dot \rho \\ \dot \alpha \\ \dot \beta \end{pmatrix} = \begin{pmatrix} - k _{\rho} \rho \cos \alpha \\ k _{\rho} \rho \sin \alpha - k _{\alpha} \alpha - k _{\beta} \beta \\ -k _{\rho} \sin \alpha \end{pmatrix} $

for the closed-loop system.

---

And yes, it looks like there may be a typo in the book (on page 76 for the first edition, presumably on page 109 in yours?)

---

A list of errata for RVC can be found on Peter's website, and this doesn't appear to be listed for either edition. I've emailed him (using the address on the errata page) to let him know about it with a link to your question.

Alternatively, Peter has recently started using Robotics:SE, so he may see it here (I've suggested an edit to the title to include the name of the book).

Answer 2

Thanks for the question and great derivation by @sempaiscuba. I first learnt about this kind of controller from the book by Siegwart etal. but the source is

Exponential Stabilization of a Wheeled Mobile Robot Via Discontinuous Control, A. Astolfi, Journal of Dynamic Systems, Measurement, and Control, March 19999, Vol 121, pp. 121-126.

---

Yes, there is an error and it should indeed be $\dot{\rho} = -k_p \rho \cos \alpha$.

There is an error in the first edition, and fixed in the second, where I mistakenly have the control inputs as $(v, \gamma)^T$, as used in @sempaiscuba's solution, rather than $(v, \omega)^T$. This control approach assumes a unicycle rather than a bicycle kino-dynamic model. The first equation on page 107 of the second edition mistakenly has $\dot{\omega}$ where it should have $\dot{y}$ is the left-hand side. I will get it right for the third edition...

I have updated the errata for the book.