How to get set the precision of the PGFPLOTS?

Question

I want to plot the a strange function which is the 'InterpolatingPolynomial' of the tanh(x):

(40*x*tanh(1/2))/11-(698249*x^3*tanh(1/2))/87318+(2517135701*x^5*tanh(1/2))/392931000-(8990599279*x^7*tanh(1/2))/3536379000+(666523661*x^9*tanh(1/2))/1178793000-(87882491*x^11*tanh(1/2))/1178793000+(2616454*x^13*tanh(1/2))/442047375-(40708*x^15*tanh(1/2))/147349125+(1024*x^17*tanh(1/2))/147349125-(32*x^19*tanh(1/2))/442047375-(15*x*tanh(1))/11+(1650809*x^3*tanh(1))/232848-(7656977201*x^5*tanh(1))/1047816000+(15347344853*x^7*tanh(1))/4715172000-(269158459*x^9*tanh(1))/349272000+(82887751*x^11*tanh(1))/785862000-(2527141*x^13*tanh(1))/294698250+(6658*x^15*tanh(1))/16372125-(508*x^17*tanh(1))/49116375+(16*x^19*tanh(1))/147349125+(80*x*tanh(3/2))/143-(1827209*x^3*tanh(3/2))/567567+(11431199701*x^5*tanh(3/2))/2554051500-(5986965079*x^7*tanh(3/2))/2554051500+(39926233*x^9*tanh(3/2))/65488500-(17379821*x^11*tanh(3/2))/196465500+(4771412*x^13*tanh(3/2))/638512875-(77416*x^15*tanh(3/2))/212837625+(6016*x^17*tanh(3/2))/638512875-(64*x^19*tanh(3/2))/638512875-(30*x*tanh(2))/143+(1888949*x^3*tanh(2))/1513512-(3240137519*x^5*tanh(2))/1702701000+(17611561711*x^7*tanh(2))/15324309000-(130451323*x^9*tanh(2))/392931000+(1695689*x^11*tanh(2))/32744250-(8810596*x^13*tanh(2))/1915538625+(148112*x^15*tanh(2))/638512875-(1312*x^17*tanh(2))/212837625+(128*x^19*tanh(2))/1915538625+(48*x*tanh(5/2))/715-(9587629*x^3*tanh(5/2))/23648625+(109639993*x^5*tanh(5/2))/170270100-(3194891431*x^7*tanh(5/2))/7662154500+(5165621*x^9*tanh(5/2))/39293100-(1447093*x^11*tanh(5/2))/65488500+(796564*x^13*tanh(5/2))/383107725-(69928*x^15*tanh(5/2))/638512875+(128*x^17*tanh(5/2))/42567525-(64*x^19*tanh(5/2))/1915538625-(5*x*tanh(3))/286+(1933049*x^3*tanh(3))/18162144-(14119093201*x^5*tanh(3))/81729648000+(4749355073*x^7*tanh(3))/40864824000-(81091903*x^9*tanh(3))/2095632000+(10896041*x^11*tanh(3))/1571724000-(1767109*x^13*tanh(3))/2554051500+(8147*x^15*tanh(3))/212837625-(698*x^17*tanh(3))/638512875+(8*x^19*tanh(3))/638512875+(60*x*tanh(7/2))/17017-(5663*x^3*tanh(7/2))/262548+(2464771*x^5*tanh(7/2))/69498000-(106900847*x^7*tanh(7/2))/4378374000+(44989*x^9*tanh(7/2))/5346000-(25313*x^11*tanh(7/2))/16038000+(45439*x^13*tanh(7/2))/273648375-(14*x^15*tanh(7/2))/1447875+(64*x^17*tanh(7/2))/221524875-(16*x^19*tanh(7/2))/4652022375-(5*x*tanh(4))/9724+(487121*x^3*tanh(4))/154378224-(53447083*x^5*tanh(4))/10216206000+(336140003*x^7*tanh(4))/91945854000-(3039931*x^9*tanh(4))/2357586000+(147211*x^11*tanh(4))/589396500-(157426*x^13*tanh(4))/5746615875+(3208*x^15*tanh(4))/1915538625-(1712*x^17*tanh(4))/32564156625+(64*x^19*tanh(4))/97692469875+(20*x*tanh(9/2))/415701-(11419*x^3*tanh(9/2))/38594556+(5040143*x^5*tanh(9/2))/10216206000-(3558293*x^7*tanh(9/2))/10216206000+(32699*x^9*tanh(9/2))/261954000-(19447*x^11*tanh(9/2))/785862000+(1789*x^13*tanh(9/2))/638512875-(38*x^15*tanh(9/2))/212837625+(64*x^17*tanh(9/2))/10854718875-(16*x^19*tanh(9/2))/206239658625-(x*tanh(5))/461890+(514639*x^3*tanh(5))/38594556000-(364919*x^5*tanh(5))/16345929600+(5839219*x^7*tanh(5))/367783416000-(21713*x^9*tanh(5))/3772137600+(5473*x^11*tanh(5))/4715172000-(619*x^13*tanh(5))/4597292700+(17*x^15*tanh(5))/1915538625-(2*x^17*tanh(5))/6512831325+(8*x^19*tanh(5))/1856156927625

It's very scary lmao but, I try to trans it into

0.9979114*x-0.3195393*x^3+0.1056912*x^5-0.02658724*x^7+0.004606668*x^9-0.0005249908*x^11+0.00003808077*x^13-0.000001675943*x^15+0.0000000405108*x^17-0.000000000410371*x^19

and put it in 'PGFPLOTS':

\documentclass{ctexart}\usepackage{tikz}\usepackage{pgfplots,xfp}\begin{figure}[h]
\centering
\pgfplotsset{width=12cm,height=7cm}
\begin{tikzpicture}
    \begin{axis}[
            title={The Runge phenomenon of the function $\tanh x$},
            xlabel={$x$},
            ylabel={$y$},
            axis x line=center,
            axis y line=center,
            every inner x axis line/.append style={->},
            every inner y axis line/.append style={->},
            xmin=-6,xmax=6
        ]
        \addplot[domain=-5:5, samples=800, color=gray,smooth,]{0.9979114*x-0.3195393*x^3+0.1056912*x^5-0.02658724*x^7+0.004606668*x^9-0.0005249908*x^11+0.00003808077*x^13-0.000001675943*x^15+0.0000000405108*x^17-0.000000000410371*x^19};
        \addplot[domain=-5.2:5.2,color=black, samples=400,very thick]{tanh(x)};
    \end{axis}
\end{tikzpicture}

\end{figure} and get the figure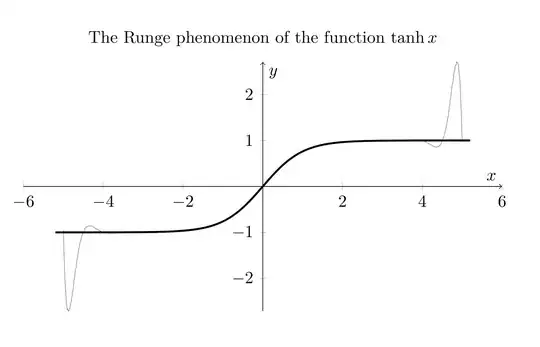

and 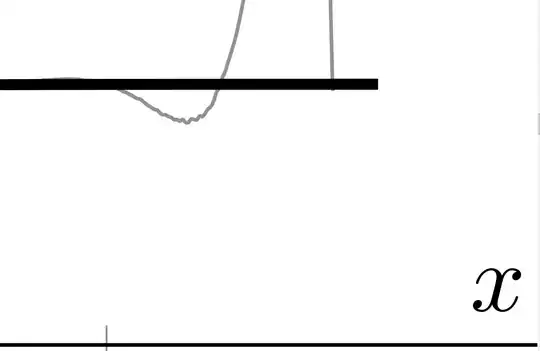this annoying 'saw' if I use the scary one:

\documentclass{ctexart}\usepackage{tikz}\usepackage{pgfplots,xfp}\begin{figure}[h]
\centering
\pgfplotsset{width=12cm,height=7cm}
\begin{tikzpicture}
    \begin{axis}[
            title={The Runge phenomenon of the function $\tanh x$},
            xlabel={$x$},legend pos = north west,
            ylabel={$y$},
            axis x line=center,
            axis y line=center,
            every inner x axis line/.append style={->},
            every inner y axis line/.append style={->},
            xmin=-6,xmax=6
        ]
        \addplot[domain=-5:5, samples=800, color=gray,smooth,]{(40*x*tanh(1/2))/11-(698249*x^3*tanh(1/2))/87318+(2517135701*x^5*tanh(1/2))/392931000-(8990599279*x^7*tanh(1/2))/3536379000+(666523661*x^9*tanh(1/2))/1178793000-(87882491*x^11*tanh(1/2))/1178793000+(2616454*x^13*tanh(1/2))/442047375-(40708*x^15*tanh(1/2))/147349125+(1024*x^17*tanh(1/2))/147349125-(32*x^19*tanh(1/2))/442047375-(15*x*tanh(1))/11+(1650809*x^3*tanh(1))/232848-(7656977201*x^5*tanh(1))/1047816000+(15347344853*x^7*tanh(1))/4715172000-(269158459*x^9*tanh(1))/349272000+(82887751*x^11*tanh(1))/785862000-(2527141*x^13*tanh(1))/294698250+(6658*x^15*tanh(1))/16372125-(508*x^17*tanh(1))/49116375+(16*x^19*tanh(1))/147349125+(80*x*tanh(3/2))/143-(1827209*x^3*tanh(3/2))/567567+(11431199701*x^5*tanh(3/2))/2554051500-(5986965079*x^7*tanh(3/2))/2554051500+(39926233*x^9*tanh(3/2))/65488500-(17379821*x^11*tanh(3/2))/196465500+(4771412*x^13*tanh(3/2))/638512875-(77416*x^15*tanh(3/2))/212837625+(6016*x^17*tanh(3/2))/638512875-(64*x^19*tanh(3/2))/638512875-(30*x*tanh(2))/143+(1888949*x^3*tanh(2))/1513512-(3240137519*x^5*tanh(2))/1702701000+(17611561711*x^7*tanh(2))/15324309000-(130451323*x^9*tanh(2))/392931000+(1695689*x^11*tanh(2))/32744250-(8810596*x^13*tanh(2))/1915538625+(148112*x^15*tanh(2))/638512875-(1312*x^17*tanh(2))/212837625+(128*x^19*tanh(2))/1915538625+(48*x*tanh(5/2))/715-(9587629*x^3*tanh(5/2))/23648625+(109639993*x^5*tanh(5/2))/170270100-(3194891431*x^7*tanh(5/2))/7662154500+(5165621*x^9*tanh(5/2))/39293100-(1447093*x^11*tanh(5/2))/65488500+(796564*x^13*tanh(5/2))/383107725-(69928*x^15*tanh(5/2))/638512875+(128*x^17*tanh(5/2))/42567525-(64*x^19*tanh(5/2))/1915538625-(5*x*tanh(3))/286+(1933049*x^3*tanh(3))/18162144-(14119093201*x^5*tanh(3))/81729648000+(4749355073*x^7*tanh(3))/40864824000-(81091903*x^9*tanh(3))/2095632000+(10896041*x^11*tanh(3))/1571724000-(1767109*x^13*tanh(3))/2554051500+(8147*x^15*tanh(3))/212837625-(698*x^17*tanh(3))/638512875+(8*x^19*tanh(3))/638512875+(60*x*tanh(7/2))/17017-(5663*x^3*tanh(7/2))/262548+(2464771*x^5*tanh(7/2))/69498000-(106900847*x^7*tanh(7/2))/4378374000+(44989*x^9*tanh(7/2))/5346000-(25313*x^11*tanh(7/2))/16038000+(45439*x^13*tanh(7/2))/273648375-(14*x^15*tanh(7/2))/1447875+(64*x^17*tanh(7/2))/221524875-(16*x^19*tanh(7/2))/4652022375-(5*x*tanh(4))/9724+(487121*x^3*tanh(4))/154378224-(53447083*x^5*tanh(4))/10216206000+(336140003*x^7*tanh(4))/91945854000-(3039931*x^9*tanh(4))/2357586000+(147211*x^11*tanh(4))/589396500-(157426*x^13*tanh(4))/5746615875+(3208*x^15*tanh(4))/1915538625-(1712*x^17*tanh(4))/32564156625+(64*x^19*tanh(4))/97692469875+(20*x*tanh(9/2))/415701-(11419*x^3*tanh(9/2))/38594556+(5040143*x^5*tanh(9/2))/10216206000-(3558293*x^7*tanh(9/2))/10216206000+(32699*x^9*tanh(9/2))/261954000-(19447*x^11*tanh(9/2))/785862000+(1789*x^13*tanh(9/2))/638512875-(38*x^15*tanh(9/2))/212837625+(64*x^17*tanh(9/2))/10854718875-(16*x^19*tanh(9/2))/206239658625-(x*tanh(5))/461890+(514639*x^3*tanh(5))/38594556000-(364919*x^5*tanh(5))/16345929600+(5839219*x^7*tanh(5))/367783416000-(21713*x^9*tanh(5))/3772137600+(5473*x^11*tanh(5))/4715172000-(619*x^13*tanh(5))/4597292700+(17*x^15*tanh(5))/1915538625-(2*x^17*tanh(5))/6512831325+(8*x^19*tanh(5))/1856156927625};
        \addplot[domain=-5.2:5.2,color=black, samples=400,very thick]{tanh(x)};
    \end{axis}
\end{tikzpicture}\end{figure}

I get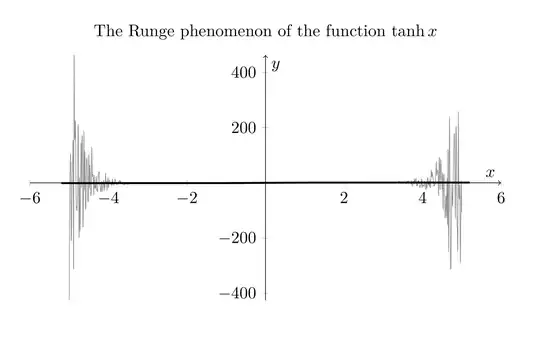 I thaught that it's the precision of PGFPLOTS made this, and how to fix them?

Answer 1

Welcome to TeX Stack Exchange! With respect to the title of your post, you should know all the package documentation is on CTAN. The pgfplots documentation is here. From the bottom of page 54 you will find,

Starting with version 1.2, \addplot expression uses a floating point unit. The FPU provides the full data range of scientific computing with a relative precision between 10^−4 and 10^−6. The /pgf/fpu key provides some more details.
Note that pgfplots makes use of lualatex’s features: if you use lualatex instead of pdflatex, pgfplots will use lua’s math engine which is both faster and more accurate (compat=1.12 or higher).

You can also search this site to find questions that might be similar or relevant to yours.

From your function and its "simplification", I'm sure you know that there is a difference between using a calculator, scientific calculator, CAS, or computer in doing your calculations. Given the complexity of your function (with 9 digit coefficients and exponents of 19), pgfplots is the wrong tool to use for complex calculations. The answer to your problem is to use the proper tool. That depends, in part, on you and your usage. Using the LuaLaTeX engine was already suggested. It can do the calculations. Some people like Asymptote. I'm partial to sagetex for several reasons:

1. It gives you access to a CAS, called Sage, which is already set to handle all sorts of mathematics from matrices to Fourier transforms to graph theory. It's similar to Mathematica, except it's free.
2. You get the Python language included in it. This makes programming easier to learn. It also means you can often find the code for your problem online.
3. Python is outstanding for working with strings. With sagetex there is no need to approximate your function; you can work with it directly.

\documentclass{article}
\usepackage{sagetex}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{sagesilent}
LowerX = -5
UpperX = 5
LowerY = -3
UpperY = 3
step = .01
Scale = 1.0
xscale=1.0
yscale=1.0
###############
output = r""
output += r"\begin{tikzpicture}"
output += r"[line cap=round,line join=round,x=8.75cm,y=8cm]"
output += r"\begin{axis}["
output += r"title={The Runge phenomenon of the function $\tanh x$},"
output += r"grid = none,"
output += r"minor tick num=4,"
output += r"every major grid/.style={Red!30, opacity=1.0},"
output += r"every minor grid/.style={ForestGreen!30, opacity=1.0},"
output += r"height= %f\textwidth,"%(yscale)
output += r"width = %f\textwidth,"%(xscale)
output += r"thick,"
output += r"black,"
output += r"axis lines=center,"
output += r"domain=%f:%f,"%(LowerX,UpperX)
output += r"line join=bevel,"
output += r"xmin=%f,xmax=%f,ymin= %f,ymax=%f,"%(LowerX,UpperX,LowerY, UpperY)
#output += r"xticklabels=\empty,"
#output += r"yticklabels=\empty,"
output += r"major tick length=5pt,"
output += r"minor tick length=0pt,"
output += r"xlabel={$x$},ylabel={$y$},"
output += r"major x tick style={black,very thick},"
output += r"major y tick style={black,very thick},"
output += r"minor x tick style={black,thin},"
output += r"minor y tick style={black,thin},"
#output += r"xtick=\empty,"
#output += r"ytick=\empty"
output += r"]"
######################## FUNCTION
var('t')
f(x)=(40*x*tanh(1/2))/11-(698249*x^3*tanh(1/2))/87318+(2517135701*x^5*tanh(1/2))/392931000-(8990599279*x^7*tanh(1/2))/3536379000+(666523661*x^9*tanh(1/2))/1178793000-(87882491*x^11*tanh(1/2))/1178793000+(2616454*x^13*tanh(1/2))/442047375-(40708*x^15*tanh(1/2))/147349125+(1024*x^17*tanh(1/2))/147349125-(32*x^19*tanh(1/2))/442047375-(15*x*tanh(1))/11+(1650809*x^3*tanh(1))/232848-(7656977201*x^5*tanh(1))/1047816000+(15347344853*x^7*tanh(1))/4715172000-(269158459*x^9*tanh(1))/349272000+(82887751*x^11*tanh(1))/785862000-(2527141*x^13*tanh(1))/294698250+(6658*x^15*tanh(1))/16372125-(508*x^17*tanh(1))/49116375+(16*x^19*tanh(1))/147349125+(80*x*tanh(3/2))/143-(1827209*x^3*tanh(3/2))/567567+(11431199701*x^5*tanh(3/2))/2554051500-(5986965079*x^7*tanh(3/2))/2554051500+(39926233*x^9*tanh(3/2))/65488500-(17379821*x^11*tanh(3/2))/196465500+(4771412*x^13*tanh(3/2))/638512875-(77416*x^15*tanh(3/2))/212837625+(6016*x^17*tanh(3/2))/638512875-(64*x^19*tanh(3/2))/638512875-(30*x*tanh(2))/143+(1888949*x^3*tanh(2))/1513512-(3240137519*x^5*tanh(2))/1702701000+(17611561711*x^7*tanh(2))/15324309000-(130451323*x^9*tanh(2))/392931000+(1695689*x^11*tanh(2))/32744250-(8810596*x^13*tanh(2))/1915538625+(148112*x^15*tanh(2))/638512875-(1312*x^17*tanh(2))/212837625+(128*x^19*tanh(2))/1915538625+(48*x*tanh(5/2))/715-(9587629*x^3*tanh(5/2))/23648625+(109639993*x^5*tanh(5/2))/170270100-(3194891431*x^7*tanh(5/2))/7662154500+(5165621*x^9*tanh(5/2))/39293100-(1447093*x^11*tanh(5/2))/65488500+(796564*x^13*tanh(5/2))/383107725-(69928*x^15*tanh(5/2))/638512875+(128*x^17*tanh(5/2))/42567525-(64*x^19*tanh(5/2))/1915538625-(5*x*tanh(3))/286+(1933049*x^3*tanh(3))/18162144-(14119093201*x^5*tanh(3))/81729648000+(4749355073*x^7*tanh(3))/40864824000-(81091903*x^9*tanh(3))/2095632000+(10896041*x^11*tanh(3))/1571724000-(1767109*x^13*tanh(3))/2554051500+(8147*x^15*tanh(3))/212837625-(698*x^17*tanh(3))/638512875+(8*x^19*tanh(3))/638512875+(60*x*tanh(7/2))/17017-(5663*x^3*tanh(7/2))/262548+(2464771*x^5*tanh(7/2))/69498000-(106900847*x^7*tanh(7/2))/4378374000+(44989*x^9*tanh(7/2))/5346000-(25313*x^11*tanh(7/2))/16038000+(45439*x^13*tanh(7/2))/273648375-(14*x^15*tanh(7/2))/1447875+(64*x^17*tanh(7/2))/221524875-(16*x^19*tanh(7/2))/4652022375-(5*x*tanh(4))/9724+(487121*x^3*tanh(4))/154378224-(53447083*x^5*tanh(4))/10216206000+(336140003*x^7*tanh(4))/91945854000-(3039931*x^9*tanh(4))/2357586000+(147211*x^11*tanh(4))/589396500-(157426*x^13*tanh(4))/5746615875+(3208*x^15*tanh(4))/1915538625-(1712*x^17*tanh(4))/32564156625+(64*x^19*tanh(4))/97692469875+(20*x*tanh(9/2))/415701-(11419*x^3*tanh(9/2))/38594556+(5040143*x^5*tanh(9/2))/10216206000-(3558293*x^7*tanh(9/2))/10216206000+(32699*x^9*tanh(9/2))/261954000-(19447*x^11*tanh(9/2))/785862000+(1789*x^13*tanh(9/2))/638512875-(38*x^15*tanh(9/2))/212837625+(64*x^17*tanh(9/2))/10854718875-(16*x^19*tanh(9/2))/206239658625-(x*tanh(5))/461890+(514639*x^3*tanh(5))/38594556000-(364919*x^5*tanh(5))/16345929600+(5839219*x^7*tanh(5))/367783416000-(21713*x^9*tanh(5))/3772137600+(5473*x^11*tanh(5))/4715172000-(619*x^13*tanh(5))/4597292700+(17*x^15*tanh(5))/1915538625-(2*x^17*tanh(5))/6512831325+(8*x^19*tanh(5))/1856156927625
x_coords = [t for t in srange(-5,5.01,.01)]
y_coords = [f(t).n(digits=4) for t in srange(-5,5.01,.01)]
output += r"\addplot[thin, NavyBlue, unbounded coords=jump] coordinates {"
for i in range(0,len(x_coords)-1):
    if (y_coords[i])<LowerY or (y_coords[i])>UpperY:
        output += r"(%f , inf) "%(x_coords[i])
    else:
        output += r"(%f , %f) "%(x_coords[i],y_coords[i])
#########
output += r"};"
output+= r"\addplot[domain=-5.2:5.2,color=red, samples=400,thick]{tanh(x)};"
output += r"\end{axis}"
output += r"\end{tikzpicture}"
\end{sagesilent}
\begin{center}
\sagestr{output}
\end{center}
\end{document}

The output is shown below, running in Cocalc:

The linesx_coords = [t for t in srange(-5,5.01,.01)] and y_coords = [f(t).n(digits=4) for t in srange(-5,5.01,.01)] are using Sage (via Python) to create the x values and then accurately calculate the y values. The part n(digits=4) is taking the long decimal and cutting it down to 4 significant figures for pgfplots to plot. The for-loop after that is telling to it plot data if it is on the screen. If it falls outside of your axes, ignore it.

The downside of using sagetex is that Sage isn't part of a LaTeX distribution. You either need to download it on your computer and get it to work with your LaTeX distribution (which can be tricky) or access it with a free Cocalc account.